WYNIKI OBLICZEŃ 2- STOPNIOWEJ PRZEKŁADNI REDUKCYJNEJ TYPU „A”
MOC URZĄDZENIA NAPĘDZAJĄCEGO PRZEKŁADNIĘ REDUKCYJNĄ: 8 kW
CAŁKOWITE PRZEŁOŻENIE PRZEKŁADNI: 10
PRZEŁOŻENIE PIERWSZEJ PARY KÓŁ ZĘBATYCH: 2,99
PRZEŁOŻENIE DRUGIEJ PARY KÓŁ ZĘBATYCH: 3,35
PRĘDKOŚĆ OBROTOWA NA WAŁKU I: 6000 obr/min
MOMENT OBROTOWY NA WAŁKU I: 12,73 Nm
PRĘDKOŚĆ OBROTOWA NA WAŁKU II: 2006,6 obr/min
MOMENT OBROTOWY NA WAŁKU II: 38,07 Nm
PRĘDKOŚĆ OBROTOWA NA WAŁKU III: 599,01 obr/min
MOMENT OBROTOWY NA WAŁKU III: 127,54 Nm
KOŁA ZĘBATE:
|
I |
II |
III |
IV |
LICZBA ZĘBÓW |
17 |
51 |
17 |
57 |
MODUŁ [mm] |
2,0 |
2,0 |
2,0 |
2,0 |
ŚREDNICA PODZIAŁOWA [ mm] |
36,18 |
108,55 |
36,18 |
121,32 |
ŚREDNICA WIERZCHOŁKÓW ZĘBÓW [ mm ] |
40,18 |
112,55 |
40,18 |
125,32 |
ŚREDNICA PODSTAWY ZĘBÓW [ mm ] |
31,78 |
104,15 |
31,78 |
116,92 |
SZEROKOŚĆ WIEŃCA ZĘBATEGO [ mm ] |
30 |
30 |
30 |
30 |
WPUST PRYZMATYCZNY |
8 x 7 x 15 |
12 x 8 x 18 |
12 x 8 x 18 |
10 x 8 x 25 |
WSZYSTKIE KOŁA ZĘBATE ZOSTAŁY WYKONANE ZE STALI 35 HM Z
UZĘBIENIEM ŚRUBOWYM, KĄT POCHYLENIA LINII ZĘBA β= 20°, KĄT
LINII PRZYPORU α= 20°
WAŁEK BĘDZIE WYKONANY ZE STALI 45, DLA KTÓREJ DOPUSZCZALNE
NAPRĘŻENIA NA ZGINANIE WYNOSZĄ kgi=125 Mpa.
ŁOŻYSKA:
WAŁEK I OSADZONY BĘDZIE NA ŁOŻYSKACH JĘDNORZĘDOWYCH
STOŻKOWYCH SERII 30203
WAŁEK II OSADZONY BĘDZIE NA ŁOŻYSKACH JĘDNORZĘDOWYCH
STOŻKOWYCH SERII 30206
WAŁEK III OSADZONY BĘDZIE NA ŁOŻYSKACH JĘDNORZĘDOWYCH
STOŻKOWYCH SERII 30205
ALGORYTM OBLICZEŃ PRZEKŁADNI REDUKCYJNEJ |
Na podstawie całkowitego przełożenia przekładni redukcyjnej dobieram:
- przełożenie pierwszej pary kół zębatych, które wynosi i1= 2,99
- przełożenie drugiej pary kół zębatych, które wynosi i2= 3,35
Wyliczenie prędkości obrotowych na poszczególnych wałkach.
![]()
prędkość na wałku drugim wynosi n2= 2006,6 [obr/min]
prędkość na wałku trzecim wynosi n3= 599,01 [obr/min]
Wyznaczenie momentów obrotowych na poszczególnych wałkach.
![]()
moment obrotowy na pierwszym wałku wynosi M1= 12,73 Nm
moment obrotowy na drugim wałku wynosi M2= 38,07 Nm
moment obrotowy na trzecim wałku wynosi M3= 127,54 Nm
3. Wyznaczam ilość zębów na poszczególnych kołach zębatych .
![]()
ilość zębów koła drugiego wynosi z2= 51
ilość zębów koła trzeciego wynosi z3= 57
Obliczenie modułu pierwszej pary kół zębatych.
Kąt pochylenia linii zęba wynosi β=20 Materiał ,z którego mają być wykonane koła zębate to 35HM
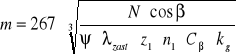
m= 0.37 mm
Na podstawie PN-78/M-88502 dobieram moduł dla pierwszej pary kół zębatych m=2.0 mm
Do obliczeń przyjmuję, że koła zębate będą miały zęby normalne, o kącie przyporu
α=20°
wykonane dość dokładnie Ψ=15
Współczynnik uwzględniający wpływ stopnia pokrycia Cβ=1,4
5. Obliczam zastępczą liczbę zębów zzast i na jej podstawie dobieram współczynnik wytrzymałości zęba λzast
![]()
Zastępcza liczba zębów wynosi zzast=20, współczynnik wytrzymałości zęba λzast=3,53
6. Obliczam dopuszczalne naprężenia zginające kg przyjmując: współczynnik bezpieczeństwa Xzj=1,9 współczynnik trwałości zęba Cc=1
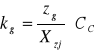
Dopuszczalne naprężenia zginające wynoszą kg=394,74 Mpa
Wytrzymałość zmęczeniowa na zginanie jednokierunkowe dobranego materiału 35HM wynosi:
zg=750 Mpa
7. Obliczam parametry geometryczne pierwszej pary kół zębatych
Koło nr I Koło nr II
Szerokość wieńca zębatego: |
|
Średnicy podziałowej: |
|
Średnicy wierzchołków zębów: |
|
Średnicy podstaw zębów: |
|
Odległość osi: |
|
8. Obliczenia wytrzymałościowe.
Sprawdzam wytrzymałość zębów u podstawy.
Określam charakter obciążenia pracy przekładni redukcyjnej: prawie bez wahań
Określam ilość godzin pracy przekładni redukcyjnej :do 12 h
• Obliczam zastępcze(całkowite) obciążenie wyrażone wzorem:
![]()
Cp=1,00, Cv=1,337, Pstat=703,704 N
• Obliczam obciążenie statyczne ze wzoru:
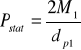
M1 - moment obrotowy na pierwszym wałku.
Pzast= 940,9 N
•Obliczam siłę obliczeniową ze wzoru:
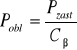
Pobl= 672,1 N
• Obliczam zastępcze naprężenie zginające ze wzoru:
![]()
δgzast= 3,17 Mpa < kg= 394,74 Mpa
• Sprawdzam wytrzymałość zębów z warunku na naciski powierzchniowe.
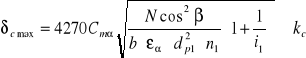
gdzie:
δc max - naciski powierzchniowe,
Cmα = 478,2 - współczynnik danej grupy materiałowej,
N - moc urządzenia napędzającego przekładnię redukcyjną,
β - kąt pochylenia linii zęba,
εα - współczynnik czołowego stopnia pokrycia,
n1 - prędkość obrotowa pierwszego wałka,
i1 - przełożenie pierwszej pary kół zębatych,
kc - dopuszczalne naprężenia na ściskanie,
![]()
εα - współczynnik czołowego stopnia pokrycia,
C1, C2, C3 - współczynniki,
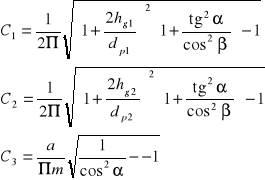
![]()
dp1 - średnica podziałowa pierwszego koła,
dp2 - średnica podziałowa drugiego koła,
hg1 - wysokość głowy zęba pierwszego koła,
hg2 - wysokość głowy zęba drugiego koła,
m - moduł,
a - odległość osi pierwszego i drugiego wałka,
α = 20° - kąt przyporu,
• Obliczam dopuszczalny nacisk wyrażony wzorem
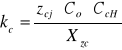
![]()
Xzc - współczynnik stanu powierzchni.
Zjc= 600 Mpa, Co=1, CcH=1, Xzc=1.188, kc= 589 Mpa
![]()
- Xzc - współczynnik stanu powierzchni
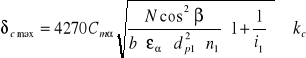
δcmax= 333 Mpa < kc=589 Mpa
Oba warunki wytrzymałościowe zostały spełnione dlatego pozostaje przy dobranym module m=2 mm dla pierwszej pary kól zębatych.
Obliczenie modułu drugiej pary kół zębatych.
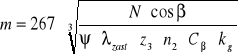
![]()
m=0,53 mm
Na podstawie PN - 78/M - 88502 dobieram moduł dla drugiej pary kół zębatych m=2,0 mm
Obliczam parametry geometryczne drugiej pary kół zębatych.
Koła nr III Koło nr IV
Szerokość wieńca zębatego: |
|
Średnicy podziałowej: |
|
Średnicy wierzchołków zębów: |
|
Średnicy podstaw zębów: |
|
Odległość osi: |
|
11.Obliczenia wytrzymałościowe wałków.
Obliczam zastępcze (całkowite) obciążenie ze wzoru:
![]()
Cp= 1,00, Cv=1,278 , Pstat= 2104,47 N
gdzie:
Pzast - obciążenie zastępcze,
Pstat - obciążenie statyczne,
Cp - współczynnik przeciążenia,
Cv - współczynnik nadwyżek dynamicznych,
![]()
v - prędkość obwodowa,
![]()
dp3 - średnica podziałowa trzeciego koła,
n2 - prędkość obrotowa drugiego wałka.
• Obliczam obciążenie statyczne ze wzoru:
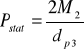
Pzast= 2690,6 N
• Obliczam siłę obliczeniową ze wzoru:
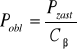
Pobl= 1921,9 N
• Obliczam zastępcze naprężenie zginające ze wzoru:
![]()
δgzast= 9,07 Mpa < kg=394,7 Mpa
b - szerokość wieńca zębatego
m - moduł ,
λzast - współczynnik wytrzymałości zęba,
kg - dopuszczalne naprężenia zginające.
• Sprawdzam wytrzymałość zębów z warunku na naciski powierzchniowe.
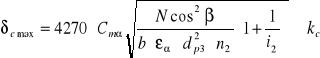
δcmax= 566 Mpa < kc= 589 Mpa
gdzie:
δc max - naciski powierzchniowe,
Cmα = 478,2 - współczynnik danej grupy materiałowej,
N - moc urządzenia napędzającego przekładnię redukcyjną,
β - kąt pochylenia linii zęba,
εα - współczynnik czołowego stopnia pokrycia,
n2 - prędkość obrotowa drugiego wałka,
i2 - przełożenie drugiego pary kół zębatych,
kc - dopuszczalne naprężenia na ściskanie.
![]()
εα - współczynnik czołowego stopnia pokrycia,
C1, C2, C3 - współczynniki,
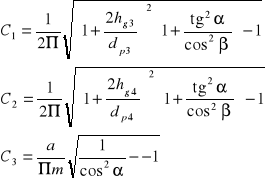
![]()
dp3 - średnica podziałowa pierwszego koła,
dp4 - średnica podziałowa drugiego koła,
hg3 - wysokość głowy zęba pierwszego koła,
hg4 - wysokość głowy zęba drugiego koła,
m - moduł,
a - odległość osi pierwszego i drugiego wałka,
α = 20° - kąt przyporu,
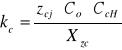
Zcj= 600 Mpa, Co=1,00, CcH=1,00, Xzc=1,188, kc= 589 Mpa
Zcj - wytrzymałość trwała na zmęczenie ściskaniem,
Co - współczynnik uwzględniający lepkość oleju,
CcH - współczynnik uzależniony od żądanej ilości wahnięć,
Xzc - współczynnik bezpieczeństwa przy zmęczeniowym nacisku,
Xzc - współczynnik stanu powierzchni
![]()
Oba warunki wytrzymałościowe zostały spełnione, dlatego pozostaje przy dobranym module m=2,0 mm dla drugiej pary kół zębatych.
Obliczenia wytrzymałościowe wałków.
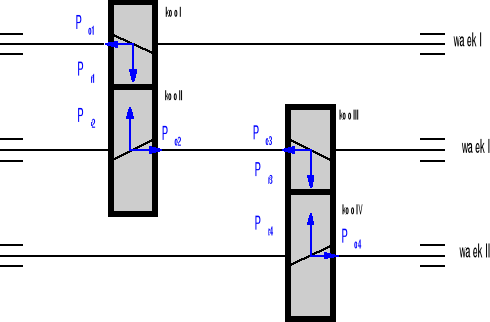
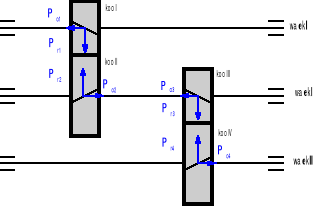
Schemat rozkładu sił w przekładni.
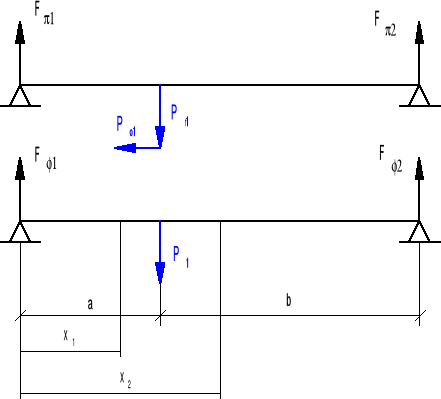
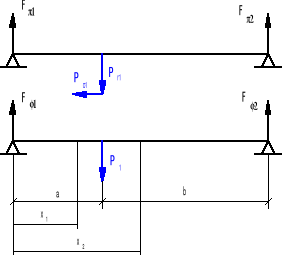
Obliczenia wałka pierwszego.
a= 40 mm
l= a + b= 120 mm
• Wyliczam siły: promieniową Pr1 i poosiową Po1 na podstawie wzorów:
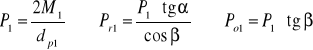
P1= 703,7 N, Pr1= 272,51 N, Po1= 256,08 N
gdzie:
M1 - moment obrotowy na pierwszym wałku,
dp1 - średnica podziałowa pierwszego koła,
Pr1 - siła promieniowa,
Po1 - siła poosiowa,
α - kąt linii przyporu,
β - kąt pochylenia linii zęba.
• Rozpatruję wałek w płaszczyźnie Π.
![]()
Fπ1= 143,0 N, Fπ2=129,4 N
• Momenty gnące:
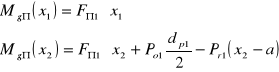
dla x1= 0, Mgπ1= 0
dla x1= a, Mgπ2= 5,72 Nm
dla x2= a, Mgπ2= 10,36 Nm
dla x2= a + b Mgπ3= 0
• Rozpatruję wałek w płaszczyźnie Φ.
![]()
Fφ1= 469,0 N, Fφ2= 234,5 N
• Momenty gnące w poszczególnych przekrojach
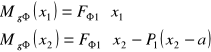
dla x1= 0, Mgφ1= 0
dla x1= a, Mgφ2= 18,77 Nm
dla x2= a, Mgφ2= 18,77 Nm
dla x2= a + b, Mgφ3= 0
• Obliczam reakcje występujące w łożyskach:
![]()
![]()
R1= 490,0 N, R2= 267,9 N
• Obliczam wypadkowy moment gnący dla poszczególnych przekrojów:
![]()
Mg1= 0, Mg2= 21,43 Nm, Mg3= 0
• Obliczam moment zastępczy dla poszczególnych przekrojów:
![]()
Mz1= 11,02 Nm, Mz2= 24,10 Nm, Mz3= 0
Wyliczam średnice wałka:
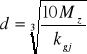
d1= 9,59 mm, d2= 12,44 mm
gdzie:
Ms - moment skręcający,
kgj - dopuszczalne naprężenia na zginanie materiału wałka
Przyjmuję średnicę pod łożyska równą: 17 mm
Przyjmuję średnicę pod koło zębate nr I równą: 27 mm
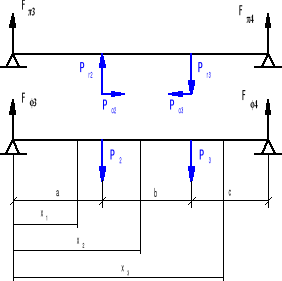
Obliczenia wałka drugiego.
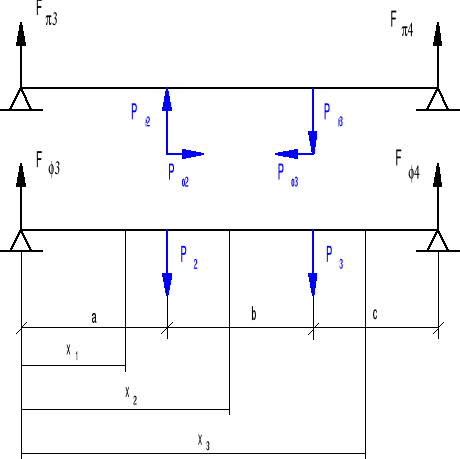
a = 40 mm b = 40 mm
l = a + b + c l = 120 mm
Wyliczam siły:
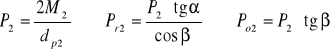
P2= 701,43 N, Pr2= 271,63 N, Po2= 255,25 N
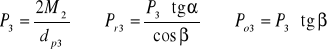
P3= 2104,4 N, Pr3= 814,97 N, Po3= 765,82 N
• Rozpatruję wałek w płaszczyźnie Π.
![]()
Fπ3= 90,57 N, Fπ4= 452,77 N
• Momenty gnące w poszczególnych przekrojach:
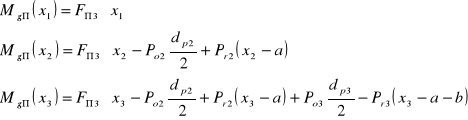
dla x1= 0, Mgπ1=0
dla x1= a, Mgπ2= 3,62 Nm
dla x2= a, Mgπ2 = -10,2 Nm
dla x2= a + b, Mgπ3= 4,26 Nm
dla x3= a + b, Mgπ3= 18,11 Nm
dla x3= a + b + c, Mgπ4= 0
• Rozpatruję wałek w płaszczyźnie Φ.
![]()
Fφ3= 1169,1 N, Fφ4= 1636,7 N
• Momenty gnące w poszczególnych przekrojach:
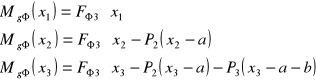
dla x1= 0, Mgφ1= 0
dla x1= a, Mgφ2= 46,76 Nm
dla x2= a, Mgφ2= 46,76 Nm
dla x2= a+ b, Mgφ3= 65,47 Nm
dla x3= a + b, Mgφ3= 65,47 Nm
dla x3= a + b + c, Mgφ4= 0
• Obliczam reakcje występujące w łożyskach:
![]()
R3= 1172,6 N R4=1698,2 N
• Obliczam wypadkowy moment gnący:
![]()
Mg1= 0, Mg2= 47,87 Nm, Mg3= 67,93 Nm, Mg4= 0
• Obliczam wypadkowy moment zastępczy dla poszczególnych przekrojów:
![]()
Mz1= 0, Mz2= 58,13 Nm, Mz3= 75,51 Nm, Mz4= 0
• Wyliczam średnice wałka:
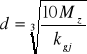
d2= 16,68 mm, d3= 23,20 mm
Przyjmuję średnicę pod łożyska równą: 30 mm
Przyjmuję średnicę pod koło zębate nr II równą: 40 mm
Przyjmuję średnicę pod koło zębate nr III równą: 40 mm
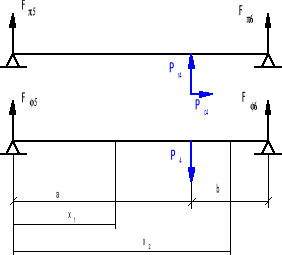
Obliczenia wałka trzeciego.
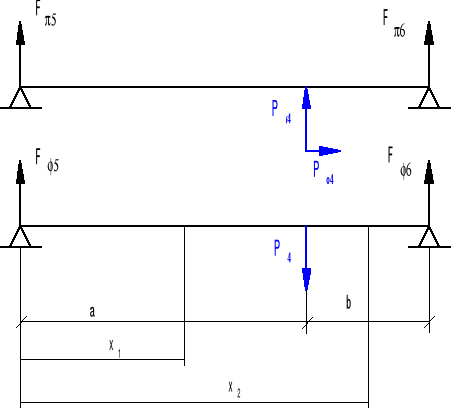
a = 80 mm l = a + b l = 120 mm
• Wyliczam siły:
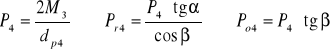
P4= 2102,5 N, Pr4= 814,2N, Po4= 765,11 N
• Rozpatruję wałek w płaszczyźnie Π.
![]()
Fπ5= 115,36 N, Fπ6= - 929,58 N
• Momenty gnące:
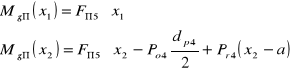
dla x1= 0, Mgπ1= 0
dla x1= a, Mgπ2= 9,23 Nm
dla x2= a, Mgπ2= - 37,1 Nm
dla x2= a + b, Mgπ3= 0
• Rozpatruję wałek w płaszczyźnie Φ.
![]()
Fφ5= 700,85 N, Fφ6= 1401,06 N
• Momenty gnące:
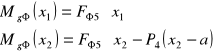
dla x1= 0, Mgφ1=0
dla x1= a, Mgφ2= 56,07 Nm
dla x2= a, Mgφ2= 56,07 Nm
dla x2= a + b, Mgφ3= 0
• Obliczam reakcje występujące w łożyskach:
![]()
R5= 710,28 N, R6= 1681,9 N
• Obliczam wypadkowy moment gnący:
![]()
Mg1= 0, Mg2= 56,82 Nm, Mg3= 0
• Obliczam moment zastępczy:
![]()
Mz1= 0, Mz2= 124,2 Nm, Mz3= 110,4 Nm
• Wyliczam średnice wałka:
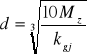
d2= 21,48 mm, d3= 20,66 mm
Przyjmuję średnicę pod łożyska równą: 25
Przyjmuję średnicę pod koło zębate nr IV równą: 35
13. Obliczenia łożysk.
• dobór łożysk na podstawie PN-86/M-86220
Dobieramy twardość łożysk tocznych wyrażoną w godzinach 8000
Ze względów konstrukcyjnych dla każdego wałka dobierane będą jednorzędowe
łożyska stożkowe.
• Obliczam obciążenie zastępcze:
![]()
obciążenie zastępcze łożysk wałka pierwszego PI= R1= 490,47 N
obciążenie zastępcze łożysk wałka drugiego PII= R4=1698,2 N
obciążenie zastępcze łożysk wałka trzeciego PIII = R6= 1681,9 N
• Obliczam nośność ruchową (łożyska):
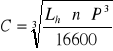
nośność łożysk wałka pierwszego CI= 6926 N .
nośność łożysk wałka drugiego CII=16632 N
nośność łożysk wałka trzeciego CIII= 11013N
• Dobieram:
Do wałka pierwszego jednorzędowe łożyska stożkowe serii 30203 dla, których
nośność ruchowa wynosi 13500 N
Do wałka drugiego jednorzędowe łożyska stożkowe serii 30206 dla, których
nośność ruchowa wynosi 27500 N
Do wałka trzeciego jednorzędowe łożyska stożkowe serii 30205 dla, których
nośność ruchowa wynosi 21000 N
14. Obliczenia wpustów pod koła zębate
Dobieram na podstawie PN - 70/M - 85005 dla danej średnicy dobieram wpust b×h.
• Pod koło zębate nr I do średnicy wałka 27 mm wpust b × h: 8 × 7
• Pod koło zębate nr II do średnicy wałka 45 mm wpust b × h: 12 × 8
• Pod koło zębate nr III do średnicy wałka 45 mm wpust b × h: 12 × 8
• Pod koło zębate nr IV do średnicy wałka 35 mm wpust b × h: 10 × 8
Zakładamy, że wszystkie wpusty będą wykonane ze stali St 7, dla której dopuszczalne
naprężenia ko= 105 Mpa
Obliczam długość wpustów:
l= lo + b lo≥ F/ t⋅ ko ko= z⋅ kc
♦ Wyliczona długość wpustu pod koło nr I wynosi: 10,25 mm, przyjmuję 15 mm
♦ Wyliczona długość wpustu pod koło nr II wynosi: 15,63 mm, przyjmuję 18 mm
♦ Wyliczona długość wpustu pod koło nr III wynosi: 15,63 mm, przyjmuję 18 mm
♦ Wyliczona długość wpustu pod koło nr IV wynosi: 23,88 mm, przyjmuję 25 mm
15.Obliczenia na zagrzanie przekładni.
Obliczam moc tarcia.
![]()
Nt= 0,17 kW
gdzie:
Nt - moc tarcia,
Nt1, Nt2 - moc tarcia pierwszej i drugiej pary kół zębatych,
N - moc przenoszona przez przekładnię,
i1, i2 - przełożenie pierwszej i drugiej pary kół zębatych,
z1, z3 - liczba zębów koła pierwszego i trzeciego.
• Sprawdzam czy warunek przed nadmiernym zagrzaniem jest spełniony:
![]()
Xt= 3,13 > 1
gdzie:
xt - współczynnik pewności,
m - moduł koła zębatego,
b - szerokość wieńca zębatego.
Warunek został spełniony, nie ma niebezpieczeństwa zagrzania.
1
4
Wyszukiwarka
Podobne podstrony:
WYNIKI OBLICZEŃ 2 STOPNIOWEJ PRZEKŁADNI REDUKCYJNEJ TYPU „A” 2
E Mazanek Przyklady obliczen z podstaw konstrukcji maszyn czesc 2
, podstawy konstrukcji maszyn II P, Przekladnia Zebata projekt
obliczenia- przkładnia, semestr 5, PKM - podstawy konstrukcji maszyn, PKM, Materiały (katalogi, wykł
obliczenia, Politechnika Lubelska, PKM- Podstawy Konstrukcji Maszyn, Projekt Podnośnik
Przekł zębat algor, PKM, PKM, PKM - Podstawy Konstrukcji Maszyn, Różne materiały
przekładnia zębata, UTP-ATR, Podstawy konstrukcji maszyn dr. R. Sołtysiak
,PODSTAWY KONSTRUKCJI MASZYN, OBLICZENIA WYTRZYMAŁOŚCIOWE
PKM projekt, Lotnictwo i Kosmonautyka WAT, semestr 3, Podstawy konstrukcji maszyn, Projekt przekładn
Przekładnia stożkowa, Podstawy konstrukcji maszyn
PKM przekładnia pasowa, Mechanika IV semestr, Podstawy Konstrukcji Maszyn UTP, laboratorium, PKM sem
pkm przekladnia sciaga, Mechanika IV semestr, Podstawy Konstrukcji Maszyn UTP, laboratorium, PKM sem
E Mazanek Przyklady obliczen z podstaw konstrukcji maszyn czesc 1
Scenariusze zajęć na metodykę zabawy, Pedagogika, Studia stacjonarne I stopnia, Rok 3, Metodyka pra
Przekładnie, Mechatronika WAT, Podstawy konstrukcji maszyn, Przekladnia Zebata
łożysko toczne i przekładnia pasowa, Podstawy Konstrukcji Maszyn
więcej podobnych podstron