00098503

Ustalmy z loles <? e (— n, +n>. natomiast r niech rataje od 0 do 1. tej odpowiada oczywiście ruch punktu z po odcinku od punktu 0 do punktu +/siny.

Rozpatrzmy lalka przypadków.

Jeżeli y = — to równania 011.99) są postaci u — 0

a więc punkt w porusza się po półprostej Rew = 0 i Im w 3* 0, od oo Jeżeli y = + _, to równania (IU.99) są postaci

W=o

—4N    '

>

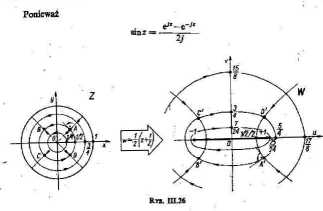
frakcja staż. Zbadamy odwzorowanie za pomocą funkcji w = slnż

a zatem punkt w porusza się po półprostej Rew = 0 i Im w < 0, od oo Podobnie dowodzimy, że dla y = 0 punkt w porusza się po półprostej i Rew > 1, od co do 1, natomiast dla y = rr punkt w porusza się Imw = ©i Rew < —1, od punktu co do —1.

Pozostał jeszcze przypadek siny »* 0 i cosy & 0. Z uwagi na żale

od ptmklu 0 do punktu cosy niu (IIL100X przebiegająca

Rys. ffl.26 ilustruje przeprowadzone oi uwagę, że ortogonalnaśi Unii rodziny argz = w przekształcanym kole |z| < 1 przenosi właściwościami odwzorowania konforemnego — na obrazy tych przekształconym.

(por. zad. 6, p. 7 tego rozdz.), więc funkcję sin z można uważać za superpozycję następujących czterech przekształceń:

1'    w,

2"    H>j = e^w‘

3°    w, = —Jw₂

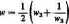
Każde z tych czterech odwzorowań jest nam znane: pierwsze i trzecie są funkcjami pierwszego stbpnia stanowiącymi obroty, drugie jest funkcją wykładniczą, czwarte natomiast jest funkcją Żukowskiego. Ponieważ funkcja pierwszego stopnia jest jednokrotna na całej płaszczyźnie, więc badając jednokrotność funkcji sinz, wystarczy zbadać jednokrotność odwzorowań 2° i 4°.

Zaczniemy od odwzorowania 2°. Wiemy, że funkcja = e”¹ jest jednokrotna w pewnym obszarze wtedy i tylko wtedy, gdy dla każdych dwóch (różnych) punktóv wj i w\' z tego obszaru oraz dla każdej liczby całkowitej k jest spełniony wanmel

*L-Wł' * 2reV

Oznaczając (por. 1”) wj ""A. w" *= A» dostajemy stąd warunek

*J—*2 * 2nk    (10.102)

Przejdźmy teraz do odwzorowania 4°. Wiemy, że funkcja Żukowskiego będąca tym odwzorowaniem jest jednokrotna w pewnym obszarze wtedy i tylko wtedy,