0408

§ 2. Funkcje uwikłane

409

D(F_i,F_z,...,F_m)

D(yi,y₂, •••.Fm) ‘

Stąd

D(F_t, F₂, ■■■, F_m)

dyi ₌    P(xi,y₂,...,y_m)

dx!    D(F_l,F₂, ...,F_m)’

D(yi,y₂,

D(Fj, F₂,    , F_m)

dy* £>(Fi,    ■■■, Xi)

D(F„F₂,...,F j-

D(yi,y₂,

Analogiczne wyrażenia otrzymuje się dla pochodnych funkcji y₁,y₂, ■■■,y_m względem zmiennych x₂,x₃,

Jeżeli funkcje F_lt F₂, F_m mają ciągłe pochodne cząstkowe rzędu drugiego, to prawe strony wszystkich otrzymanych wzorów mają ciągłe pochodne względem wszystkich argumentów, a tym samym istnieją ciągłe pochodne cząstkowe rzędu drugiego funkcji uwikłanych. Ogólnie (łatwo to dowieść indukcyjnie), istnienie ciągłych pochodnych at do rzędu k włącznie funkcji F_lt F₂,    , F_m pociąga za sobą istnienie i ciągłość wszystkich po

chodnych rzędu k funkcji uwikłanych.

Obliczenie pochodnych funkcji uwikłanych w ogólnym przypadku można także przeprowadzić albo za pomocą różniczkowania tożsamości (5) względem odpowiednich argumentów, albo przez obliczanie różniczek zupełnych. Wyznacznikiem układu równań liniowych, otrzymanego dla wyznaczenia pochodnych lub różniczek, jest zawsze różny od zera jakobian J. Uwagi te objaśnimy na przykładach.

210. Przykłady.

1) Niech y będzie związane z x równaniem

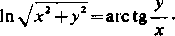
Różniczkując obie strony względem x (przy czym y traktujemy jako funkcję x), otrzymujemy

x +yy' xy'—y

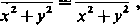
czyli x+yy'=xy'—y,

a różniczkując po raz drugi

1 +y’²+yy"=xy", itd.

Z pierwszego równania otrzymujemy a z drugiego, jeżeli podstawimy znalezioną wartość y',

__x+y

x-y

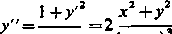
itd.

x-y    (x-y)³ ’