0420

421

§ 3. Niektóre zastosowania teorii funkcji uwikłanych

Współczynnik proporcjonalności łatwo jest obliczyć z warunku dodatkowego

a

P

e

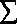
Ityfjt •

X

Jeśli stosuje się metodę Lagrange’a, trzeba zbudować funkcję pomocniczą ('):

f(<7i, <72,    <7„) = /i q_l + ... + l„q, + X¹

i przyrównać do zera jej pochodne

\

)

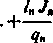
—0,

=0.

SF    X²l₁J₁

--‘1 2~

oq i    q i

dF X²l_nJ„ 3<?»

Otrzymamy stąd znowu równości (12), itd.

y²

4) Jako bardziej złożony przykład rozpatrzymy następujące zadanie. Elipsoida trójosiowa —I---h

_zi    a² b²

■f--=1 (a>b>c) jest przekrojona płaszczyzną lx+my+nz=0 przechodzącą przez jej środek. Trzeba

c²

znaleźć półosie elipsy otrzymanej w przekroju. Inaczej mówiąc, trzeba znaleźć wartości ekstremalne funkcji r² = x²+y²+z², której zmienne spełniać muszą dwa dodatkowe warunki — równania elipsoidy i płaszczyzny.

Metoda rugowania różniczek zmiennych zależnych [211] prowadzi tu do skomplikowanych rachunków, dlatego też zastosujemy od razu metodę Lagrange'a.

Aby się przekonać, że rząd macierzy

X	y	Z
~~2 a	b^2	c^7
./	m	n

jest równy 2 we wszystkich punktach przecięcia elipsoidy i płaszczyzny (²) załóżmy, że jest przeciwnie. Byłyby zatem równe zeru wszystkie wyznaczniki drugiego stopnia tej macierzy i wobec tego elementy jej pierwszego wiersza byłyby proporcjonalne do elementów drugiego wiersza. Tym samym równanie

x² y² z²

lx+my+nz = 0 pociągałoby za sobą równanie —I---1—-=0, co jest niemożliwe.

a² b² c²

Tworzymy funkcję pomocniczą

j_x² y² z² \

F(x, y, z)=x² + y² + z²+X\-j_i+^ + -^\+2iz(lx+my+nz) i przyrównujemy do zera jej pochodne

(13)    x+X -r+ji/=0 , y+X-^+/tm=0, z+X —+pn*=0 .

a    b    c

Mnożąc te równania odpowiednio przez x, y, z, dodając stronami i korzystając następnie z równań sfery i płaszczyzny, otrzymujemy X=—r².

Załóżmy, że żadna z liczb /, m, n nie jest równa zeru. Z równań (13) wynika wówczas, że r nie jest równe żadnej z liczb a, b, c i równania te możemy wobec tego napisać w postaci

x<=-n

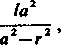
y— —p~.

mb²

z=-(i

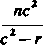
(‘) Czynnik nieoznaczony bierzemy tu dla wygody w postaci X² i włączamy do niego stałą p. (²) Zobacz uwagę w ustępie 212.