0444

§ 4. Zamiana zmiennych

445

7) Przekształcenie Legendre'a. Przytoczymy teraz znowu (por. 5) w ustępie 218) przekształcenie Legendre’a jako przykład bardziej ogólnego przekształcenia, w którym wzory wiążące stare i nowe zmienne zawierają pochodne. Wprowadźmy oznaczenia

Sz    dz    dz    dz

-    «=—,    _v = x-+y-—z.

dx    dy    dx    dy

Traktując zmienną z jako pewną określoną funkcję r=/(x, y) zmiennych * i y założymy przy tym, że dla funkcji tej spełniony jest warunek

(27)

P(t,u)J²z d²z /3^łz\² D(x,y) dx² dy² \dxdy)

Zróżniczkujmy względem x i względem y trzeci ze wzorów na przekształcenie, traktując przy tym v jako funkcję złożoną zmiennych x i y za pośrednictwem t i u. Otrzymamy

dv d²z dv d² z    d² z    d² z

dt dx²~^ du dxdy    ćx²^^ dxdy

dv d² z dv d² z d²z 3²z dt dxdy^du dy²    dxdy^^ dy²

skąd

(28)

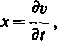
dv    dv    dv

y=—> ^a    z=t — + u -—v.

du    dt    du

Rozpatrywane przekształcenie jest zatem symetryczne względem obu trójek zmiennych x, y, z i /, u, v.

Różniczkując pierwsze dwa ze wzorów (28) najpierw względem x, a następnie względem y, otrzymujemy równania

d¹ v    d² z d² v    d² z    d²v    d² z d²v    d² z

di¹    dx²^dtdu    dxdy'    dtdu    dx²^ du²    dxdy-

oraz

d²v d²z ó²v d² z dt² dxdy^ dtdu dy²’ d²v d²z d²v d²z dtdu dxdy^du² dv²

Ponieważ [203, (4)]:

d²v d^zv / d²v \² D(x,y) 1 dt² du² \dtdu)    D(t, u) J ^

d²z

d?

d^2v		d^2v	d^2v
du^2	d^2z	dtdu	d^2z d?
	dxdy	T'	dy^2 T

z równań tych obliczamy

Traktujmy teraz x, y,z ił, u, a jako współrzędne punktów w przestrzeni. Przekształcenie Legendre’a możemy rozpatrywać jako przekształcenie przestrzeni (ale nie punktowe). Powierzchnia określona zależnością między z a x i y przechodzi przy tym przekształceniu w powierzchnię określoną zależnością między v a / i u. Ponieważ t, u, v, dv/dt, dujdu zależą tylko od x, y, z, dzjdx, dzidy, więc przekształcenie Legendre'a zachowuje styczności¹).

(‘) Można tu powtórzyć uwagę z notki na str. 434.