0530

531

Zagadnienie przedłużania funkcji

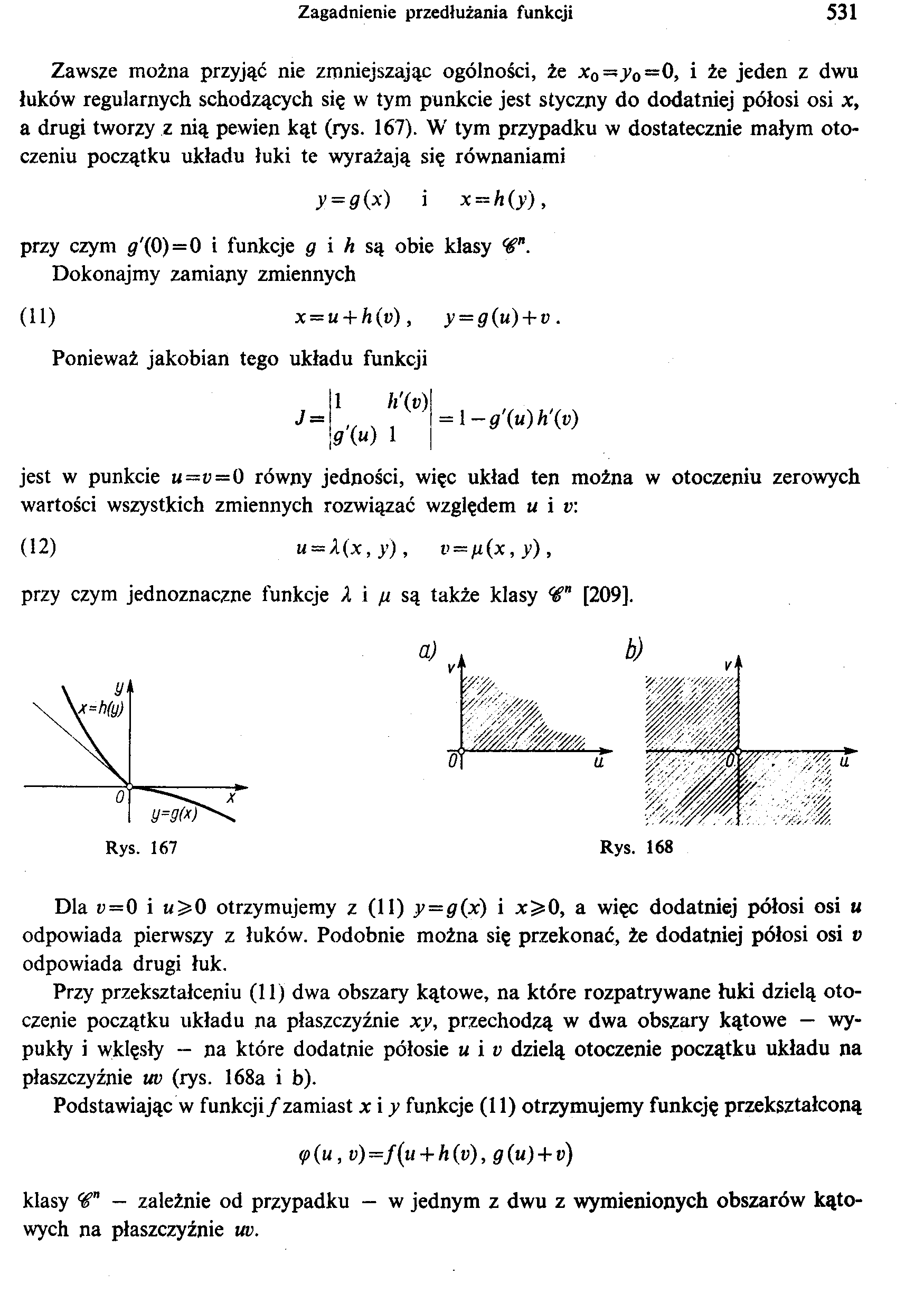
Zawsze można przyjąć nie zmniejszając ogólności, że x_o=j_o=0, i że jeden z dwu luków regularnych schodzących się w tym punkcie jest styczny do dodatniej półosi osi x, a drugi tworzy z nią pewien kąt (rys. 167). W tym przypadku w dostatecznie małym otoczeniu początku układu łuki te wyrażają się równaniami

y = 9(x) i x — h(y),

przy czym gr'(0)=0 i funkcje g i h są obie klasy ^<€ⁿ. Dokonajmy zamiany zmiennych

(11)

x = u + h(v), y = g(u) + v.

Ponieważ jakobian tego układu funkcji

|l h'(v)

!g'(u) i

= 1 -g'(u)h'(v)

jest w punkcie m=u=0 równy jedności, więc układ ten można w otoczeniu zerowych wartości wszystkich zmiennych rozwiązać względem u i v:

(12)

u = X(x,y), v — fi(x,y),

przy czym jednoznaczne funkcje X i n są także klasy [209].

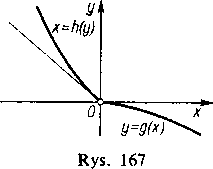
Dla v=0 i n^O otrzymujemy z (11) y=g(x) i x>0, a więc dodatniej półosi osi u odpowiada pierwszy z łuków. Podobnie można się przekonać, że dodatniej półosi osi v odpowiada drugi łuk.

Przy przekształceniu (11) dwa obszary kątowe, na które rozpatrywane łuki dzielą otoczenie początku układu na płaszczyźnie xy, przechodzą w dwa obszary kątowe — wypukły i wklęsły - na które dodatnie półosie u i v dzielą otoczenie początku układu na płaszczyźnie uv (rys. 168a i b).

Podstawiając w funkcji /zamiast x i y funkcje (11) otrzymujemy funkcję przekształconą

<p(u,v)=f(u + h(v), g(u) + v)

klasy W — zależnie od przypadku — w jednym z dwu z wymienionych obszarów kątowych na płaszczyźnie w.