20121030142

Twierdzenie Stokesa
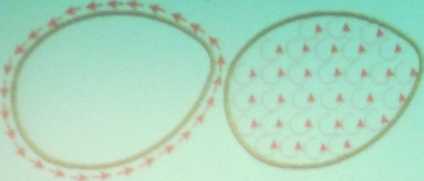
(twierdzenie o rotacji) cyrkulacja wektora K po konturze L jest równa strumieniowi rotacji tego wektora przez płat A.
j K -dl = f (rotK )• dA
Qdy
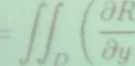
Rdz
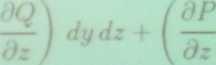
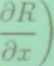
dzdx +
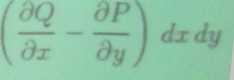
Wyszukiwarka
Podobne podstrony:
CCF20120509�070 v łV‘1v i uu
HPIM5398 Z definicji F=U-TS wynika, że pochodna cząstkowa energii swobodnej po objętości jest równa
mech2 146 290 to znaozy prędkość oiała po odbioiu jest równa pr.ędkośoi przed uderzeniem, lecz przec
mech2 146 290 to znaozy prędkość oiała po odbioiu jest równa pr.ędkośoi przed uderzeniem, lecz przec
Twierdzenie Stokesa (twierdzenie o rotacji) wiąże całkę krzywoliniową z funkcji wektorowej K po
(twierdzenie o rotacji) wiąże całkę Krzywoliniową z funkcji wektorowej K po zamkniętym konturze L z
SNC00110 7. Cyrkulacja wektora indukcji magnetycznej B po konturach oznaczonych przez Cl C2 C3,
25 (138) Twierdzenie 2.Jeżeli pole wektorowe jest rotacją pola wektorowego, to jest to pole bezźródł
Dziawgo; Wyznacznik i rząd macierzy 3 62 Wyznacznik i rząd macierzyRozwiązanie: I sposób: Korzystamy
3 analiza 14. Sprawdzić twierdzenie Stokes’a dla pola W = [y2,1, xyz] i płata S, k
D twierdzić ck» cz 40 po przyklejeniu całej nadbudówki do pokładu (da to możliwość symetryczneg
więcej podobnych podstron