8 9

8

/ = l_m • sina*

TT

czyli u = L • cal ■ cos (ot = coL • /,

u.t

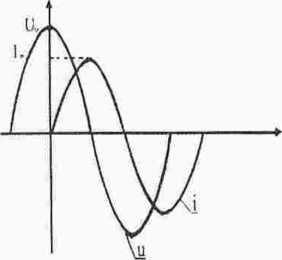
Napięcie na zaciskach cewki ,.u“’ wyprzedza w fazie przepływający przez nią prąd „i’’ o kąt

n    .....

fazowy (p — — . a jeżeli wielkością wyjściową

jest napięcie - prąd ..i” spóźnia się w stosunku 7t

do napięcia „u" o kąt (p — — .

Dla wartości skutecznych

l: = (oL ■ I = Xp ■ 1

gdzie X'l — (ol- — 2TC f L to opór bierny ndukcyjny (reaktancja

indukcyjna); jednostka oni

[X,J=s‘-H=s^l-Os= n

Reasumując

Pod wpływem prądu zmiennego w cewce indukuje się sem samoindukcji przeciwdziałająca prądowi. W efekcie prąd jest opóźniony względem napięcia oraz wytwarza się dodatkowa oporność dla prądu zmiennego (Xi.).

h) cewka rzeczywista; prócz indukcyjności uwzględniony jest również wpływ rezystancji

i

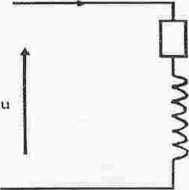
Jeżeli w obwodzie płynie prąd sinusoidalny

i = l„, • sin (ot

na zaciskach cewki indukuje się silą elektromotoryczna samoindukcji

di

e, = -L —

^Z' dl

- według II prawa Kirchllplla (dla wartości chwilowych)

u + e_L = R • i

stąd napięcie na zaciskach cewki (dla wartości chwilowych)

u = R ■ i +    = u R + u i = R • l_m • sin coi + coL ■ I_m • sin^atf + y j = CJ_m • sin [cot + <p)

gdzie:

ll|< ⁼ R-I_t„-Sill rut - napięcie na rezystancji', w fazie z prądem, o amplitudzie U_mu⁼I_m-R

u_L=©L-I_m •sili (wl+7r/2) - napięcie na indukcyjności; wyprzedza prąd o kąt 1‘azowy tp—Jt/2 o amplitudzie U,„L⁼CoL‘l_m

- według II prawa Kirchhoffu (dla wartości skutecznych) napięcie na zaciskach cewki

u =VR +UL

gdzie:

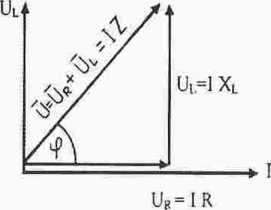
U_r-R-I - napięcie na rezystancji; wektor napięcia : ,.L’k" w luzie z wektorem prądu

U| =CdL-I - napięcie na indukcyjności: wektor napięcia ..IV’ wyprzedza wektor prądu ..I” o kąt fazowy C|>=7T/2

Wartość napięcia na zaciskach wyznaczona z trójkąta napięć:

U = ylu%+L'l =yl(m)² +{JcoL)² =l^R²+xl =I-Z

Wartość kata tp można wyznaczyć z zależności

U _L

^<P = jj^L = ^UR

IX_L_X_L coL I-R R R

Z trójkąta napięć można otrzymać trójkąt oporności: gdzie:

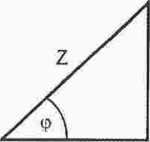
R[0] - rezystancja

X_L ⁼ f.oL = 27T fL [Q] - reaktancja indukcyjna

I 2    *2

Z=^JR + .\ i |Q)-impedaneja, ..opór''

całkowity uwzględniający rezystancję i reaklancję

R