CCF20110115012

Analiza stateczności nasypu na podłożu organicznym 5

Tabela 1 Podział metod analizy granicznej.

Metoda	Powierzchnia cylindryczna	Powierzchnia niecylindryczna	Równowaga momentów	Równowaga sił	Założenia dotyczące sił międzypaskowych
Szwedzka	*		*		Wypadkowa równoległa do podstawy paska
Bishopa	*	(!)	*		Poziome
Janbu uproszczona	(*)	*		*	Poziome
Spencera	*	(*)	*	*	Stałe nachylenie
Morgenstema- Price’a	*	*	*	*	X/E = Z-f(x)
Janbu dokładna	*	*	*	*	Zdefiniowana linia ciśnień
Fredlunda-Krahna (GLE)	*	*	*	*	X/E = Z-f(x)

2.3.1. Metoda szwedzka

Metoda szwedzka [6,7] jest najprostszą metodą pasków, umożliwiającą nawet obliczenia odręczne. Podstawowe założenie brzmi, że wypadkowa Q sił działających na boki paska Z_L, Z_R (rys. 2.1) wywołuje moment tylko dla danego paska. Ze względu na wewnętrzny charakter działania sił międzypaskowych ich moment względem dowolnego punktu musi być równy zero. Takie założenie powoduje, że kierunek działania siły Q jest równoległy do podstawy rozpatrywanego paska. Zatem wartość siły normalnej P po zsumowaniu rzutów sił na kierunek normalny do podstawy paska będzie zależna jedynie od ciężaru paska:

P = W - cos a

Obliczenie zsumowanych dla całej bryły momentów sił względem środka obrotu doprowadza do wyznaczenia współczynnika stateczności F_m.

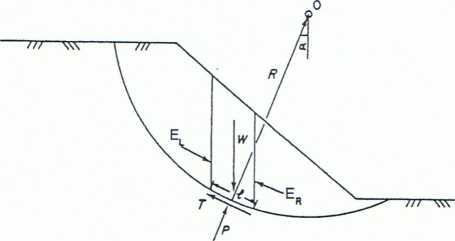
Rys. 2.1. Założenia w metodzie szwedzkiej

Właściwości gruntu: c\ </>’, y

W podstawie paska:

całkowite naprężenie normalne a,