egzamin poprawkowy 05

AGH - WYDZIAŁ IMiR ROK I D EGZAMIN Z MATEMATYK! TERMIN POPRAWKOWY II KRAKÓW 11 . 03.2005

1 . a) Podaj twierdzenie o działaniach arytmetycznych oa granicach ciągów.

b) Oblicz granice ] jpftj-r !

2    a) Podaj definicję pochodnej f

%

bl Oblicz na podstawie definicji pochodną funkcji v ~ -?= w punkcie x, =

Vx

3    a) Podaj twierdzenie o związku między istnieniem pochodne; funkcji y i⁽xi

w punkcie x₀ a jej ciągłością w rym punkcie. Czy twierdzenie odwrotne jest prawdziwe -odpowiedźuzasadnij.

2:<

b) Napisz równania lewej i prawej stycznej do krzywe; v = aresin ^ —r w pkcie r_c = J

4    ai Podaj twierdzenie dc riłosnitała.

..    (' Z 'l

b) Oblicz granicę : lim,    i^;

* \    V-OSrl/

5    a) Podaj i udowodnij rwierdzenie o związku drugiej pochodne: funkcji y =f<x;

z jej wypukłością .

b; Wyznacz przedział, w- którym funkcja /(x) - 4 v • - jest rosr.ącz t wypukła ku dołowi

U

6    a) Podaj definicję całki oznaczonej : J f(x)clx

J

b) Oblicz całkę oznaczoną

i

dc

x'

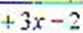
7 Stosując rachunek całkowy oblicz pole koła o promieniu r