mat


AGH - WYDZIAŁ IMiR ROK IC i ID -EGZAMIN PO-HAWKOWY Z MATEMATYKI' TERMIN I
KRAKÓW 27. C6 .2005
! .a) Podaj definicję wyznacznika macierzy A (uwzględnij wymiar macierzy }. Podaj trzy wGsoości wyznaczników . bjKorzysrąiąc z własności wy znaczników oblicz wyznacznik macierzy7:
'l 0 0 0 5]
/
0 2 0 4 O,
j j j j
0 4 0 2 0 .
_5 "0 0 0 ij
2a) Podaj definicję iloczynu wektorowego wektorów u i v . oraz interpretację jego długości Posługując się tą interpretacją wyprowadź wzór na odległość punktu P,j(”c..Y:;.r.-} cd prostej w przestrzeni RJ.
b) Napisz równanie prostej przechodzącej przez początek układu współrzędnych
i przez punkt przecięcia prostych : /.:
x - i
• = - eraz/.:
■3' - 1
-t W 1 V -r 11 ; - r
3 a ) W przestrzeni R" określona jest funkcja r ~f(x.y) , dany jest punki P.(x.- ,yi) oraz
wektor ,v[i7,ój . Podaj definicję pochodnej kierunkowej zadanej funkcji w punkcie ?a w kierunku podanego wektora. . ___
b; Oblicz pochcdną-rar.kąii. :/ =;;v rf - .ryz w punkcie M( 1,1.2). w kierunku
■ / ’* -TT —
J tworzącym z osiami układu współrzędnych kąty odpowiednio : -jK—.
3 4 3
4 1 a) Co to jest forma kwadratowa? Co tc znaczy, że ferma kwadratowa jest dodatnio
określona w zbiorze X ' _. yzrr
b) Zbadaj istnienie ekstremów funkcji: u = x* -y - z' - 2x - óyz.
5 a) Co to jest gradient funkcji r :-'y.nnzrzni_.zzzz:n

Podaj wzór i zastosowanie różniczki zupełnej I-go rzędu., b) Korzystając z różniczki funkcji obiicz przybliżoną wartość wyrażenia:
V . {io2f-90Ji. '■ K CtSi
. - - -A ,;r•_,Cćt-.._ _ _
6 a) Zdefiniuj obszar normalny Do* względem osi Ort podaj twierć^teyKKK
' o zamianie całki podwójnej funkcji _ z =-j(x,y) po ty m ccszaize: naitererwaną
b) Oblicz całkę oęćwćjna || KirA’ po obszarze D oaradczcnymfpah
oraz prostymi x - 0 i y ~ l\
7 a) Podaj twierdzenie o zmianie zmiennych w całce podwójnej, b) Obiicz całkę podwójna: /r'"
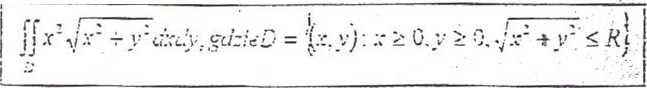
Wyszukiwarka
Podobne podstrony:
egzamin 05 termin B IIsemetr AGH - WYDZIAŁ IMiR ROK IC i ID EGZAMIN Z MATEMATYKI TERMIN BKRAKÓW
2007 egzamin AGH - WYDZIAŁ IMiR ROK I li i II EGZAMIN /. MA I ematyki KRAKÓW 9 1.1 JTY
2007 arkusz02 02 2007 AGH - WYDZIAŁ IMiR ROK IE i IF EGZAMIN Z MATEMATYKI KRAKÓW 2 LUTY
2004 poprawkowy AGH - WYDZIAŁ IMiR ROK ID n EGZAMIN POPRAWKOWY Z MATEMATYKI KRAKÓW 12.03.2004
2007 poprawkowy II AGH - WYDZIAŁ IMiR ROK IE i II II EGZAMIN POPRAWKOWY Z MATEMATYKI KRAKÓW 2 MARZ
więcej podobnych podstron