image 040

40 Fizyczne i wirtualne źródła pola promieniowania

powym można zapisać dla amplitud zespolonych w postaci:

V x E	= —jupH	(2.1)
VxH	= J + jueE	(2.2)
	= 0	(2.3)
V • D	= P	(2.4)

W przypadku anten, elementów o złożonej strukturze, korzystamy również z warunków brzegowych, które opisują zachowanie się składowych stycznych i normalnych pól na granicy Q(r) = const dwóch różnych ośrodków. W przypadku istnienia takiej granicy (rys. 2.1) uzyskujemy dla przebiegów zmiennych

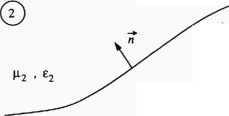
Q( r ) = const

Rys. 2.1. Ilustracja graficzna nieciągłości parametrów ośrodka

o. •^e, o

związki powszechnie znane jako warunki brzegowe:

n-{D2- Di) = ps	(2.5)
n ■ (B2 — Bi) = 0	(2.6)
n x (E2 - Ei) — 0	(2.7)
n x (H2 — H\) = Js	(2.8)

gdzie wektory natężeń i indukcji są zadane przy powierzchni granicznej, ładunki i prądy występują zaś na powierzchni granicznej.

W tym miejscu warto poczynić trzy istotne uwagi. Pierwsza dotyczy związku pomiędzy warunkami brzegowymi dla składowych stycznych i normalnych. Należy pamiętać, że spełnienie warunków dla składowych stycznych pól powoduje automatycznie spełnienie warunków dla składowych normalnych. W efekcie, formułując problem elektrodynamiczny wykorzystuje się praktycznie tylko równania dla składowych stycznych pól. Druga uwaga dotyczy występującej często w technice antenowej granicy metal-dielektryk (przybliżamy ją zwykle granicą: idealny dielektryk-ścianka elektryczna). Przypomnijmy więc, że wewnątrz idealnego przewodnika nie może istnieć pole e-m, a wiec zgodnie z (2.7) i (2.8) przy granicy idealnego przewodnika nie może istnieć składowa