image 044

44 Fizyczne i wirtualne źródła pola promieniowania

44 Fizyczne i wirtualne źródła pola promieniowania

7rl²

4 A Sfazy

odległością r a błędem fazy wynikającym z przyjęcia zależności uproszczonej (2.18):

(2.21)

Z wielu badań przeprowadzonych dla większości stosowanych anten wynikło, że przyjęcie maksymalnego błędu fazy óf_azy = 7r/8 nie prowadzi do istotnych błędów w określeniu rozkładu pola. Wprowadzając to kryterium do (2.21) uzyskujemy warunek:

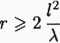
(2.22)

Warunek (2.22) wyznacza tzw. strefę daleką (zwaną również strefą Fraunho-fera), dla której błąd określenia fazy nie przekracza 7t/8 oraz, co jest bardziej istotne z praktycznego punktu widzenia, dla której można zdefiniować charakterystykę promieniowania. Warto przy tym pamiętać, że nie jest to granica „ścisła” w tym sensie, że przed i za nią mamy do czynienia z skokową zmianą wartości pola. Jest to raczej pewna umowna granica, poza którą z pewnym niewielkim błędem możemy określić pole e-m stosując uproszczenie (2.18). W przypadku anten aperturowych jako wymiar l przyjmuje się największy z wymiarów i tak np. dla apertury prostokątnej będzie to jej przekątna.

W dalszej analizie zagadnień antenowych odnoszących się do strefy dalekiej będziemy korzystać z tzw. przybliżenia strefy dalekiej, czyli pewnych uproszczeń znacznie ułatwiających znalezienie przybliżonego rozkładu pola w dużej odległości od anteny. Jest oczywistym, że takim uproszczeniem będzie zastosowanie (2.18) zamiast (2.13). Warto jednak zauważyć, że odległość R może wystąpić w czynniku fazowym kR lub jako odległość (np. w mianowniku zależności opisujących składowe pól (2.11)). W przypadku amplitud nie popełnimy większego błędu jeśli zastosujemy bardziej „grubą” aproksymację i pominiemy składnik zawierający czynnik cos#. W ten sposób uzyskujemy podstawowe uproszczenia, które będziemy stosować do analizy pól w strefie dalekiej:

R ~ r —z'cos 6 dla czynników fazowych    (2.23)

R « r    dla czynników amplitudowych    (2.24)

W bardziej ogólnym przypadku, gdy obszar, w którym są rozmieszczone źródła nie pokrywa się z osią z, zależność (2.23) przybiera postać:

(2.25)

R « r -r cos (

gdzie £ jest kątem zawartym pomiędzy wektorami r ir'.