Image3205
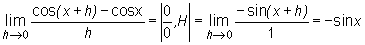
y cos(x + h) - cosx ń-> o h
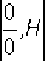
lim ń-> o
-sinfx + /?J
i
-sinx
Wyszukiwarka
Podobne podstrony:
Image3205 y cos(x + h) - cosx ń-> o h lim ń-> o -sinfx + /?J i -sinx
Image1827 x = 2arctgf, dx = 2 dt 2 sin sinx =- • 2 x sin — 2 x cos — 2 cos cosx = 2 2 X cos — 2
Oblicz granicę Rozwiązanie: lim cos x = cos 0 x—»0 1 > .. cosx lim ——— ®->0
Image1955 g) lim x-»0 X+l)e* cosx h) lim -== x^"“ Vx2 + 1 Wsk. J x dla x > O j-x dlax<0
Image3005x Na koniecobliczmy lim —5- . WtymprzypadkutwierdzeniedeTHospitala musimy zastosować kilka
Image3959 b) y = In cosx, dla xe
IMG 29 i Zadania 1 c) lim (cos x) x ; ... x — arctgrr e) lim- *->0 x2 d) lim x arc ctgz; X—►OO
egzamin2 2 i I 4 2. 3. l
ROZWIĄZANIE ZADANIA 7. Rozwiązując równanie mamy: 2cos2 x - cos* = 0, cosx(2cosx-l) = 0, stąd cos x
88663 IMG 25 155 = lim x — srnz g I h -I = lim 1 — cos: *—»o x smi o *-«o 2xsinx + *2 cos* o sin* =
IMG 29 i Zadania 1 c) lim (cos x) x ; ... x — arctgrr e) lim- *->0 x2 d) lim x arc ctgz; X—►OO
sin x = cos X m- cosx (cos X) = - sin x II s* (tg x) * = 1 / cos2 X x*n/2+ kn dla /c C c
więcej podobnych podstron