img013

W powyższym przykładzie liczba 452 oznacza ilość tych pacjentów, u których stwierdzono grupę A. Liczbę tę (jak i pozostałe z tej kolumny tabeli 2.1) nazywamy liczebnością albo częstością. Ponieważ wszystkich badanych pacjentów było 1114, więc 452

interesować nas będzie stosunek = 0,409 zwany częstością względną albo frakcją

lub czasem udziałem względnym. Czasami operujemy także udziałami procentowymi (por.ostatnią kolumnę tabeli 2.1)

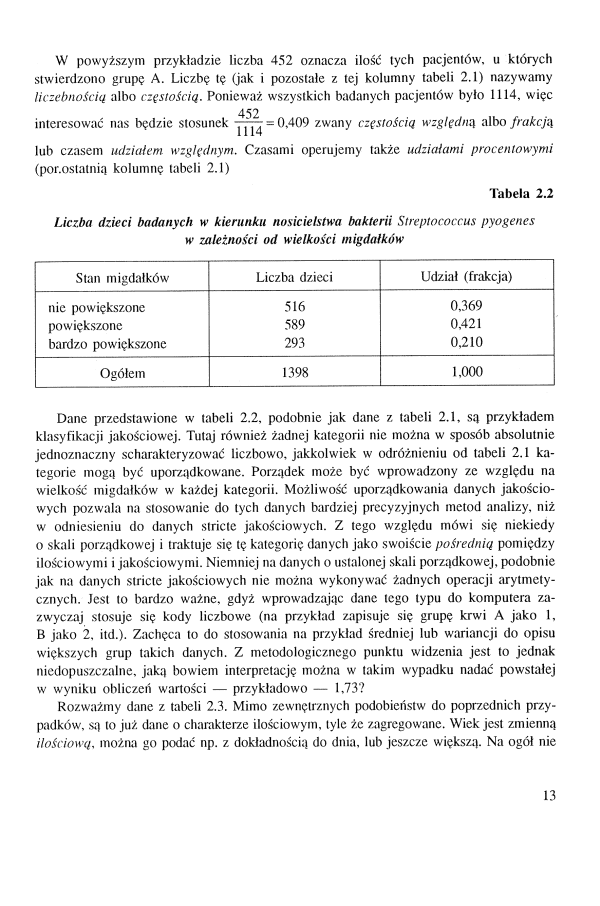
Tabela 2.2

Liczba dzieci badanych w kierunku nosicielstwa bakterii Streptococcus pyogenes w zależności od wielkości migdałków

Stan migdałków	Liczba dzieci	Udział (frakcja)
nie powiększone	516	0,369
powiększone	589	0,421
bardzo powiększone	293	0,210
Ogółem	1398	1,000

Dane przedstawione w tabeli 2.2, podobnie jak dane z tabeli 2.1, są przykładem klasyfikacji jakościowej. Tutaj również żadnej kategorii nic można w sposób absolutnie jednoznaczny scharakteryzować liczbowo, jakkolwiek w odróżnieniu od tabeli 2.1 kategorie mogą być uporządkowane. Porządek może być wprowadzony ze względu na wielkość migdałków w każdej kategorii. Możliwość uporządkowania danych jakościowych pozwala na stosowanie do tych danych bardziej precyzyjnych metod analizy, niż w odniesieniu do danych stricte jakościowych. Z tego względu mówi się niekiedy o skali porządkowej i traktuje się tę kategorię danych jako swoiście pośrednią pomiędzy ilościowymi i jakościowymi. Niemniej na danych o ustalonej skali porządkowej, podobnie jak na danych stricte jakościowych nie można wykonywać żadnych operacji arytmetycznych. Jest to bardzo ważne, gdyż wprowadzając dane tego typu do komputera zazwyczaj stosuje się kody liczbowe (na przykład zapisuje się grupę krwi A jako 1, B jako 2. itd.). Zachęca to do stosowania na przykład średniej lub wariancji do opisu większych grup takich danych. Z metodologicznego punktu widzenia jest to jednak niedopuszczalne, jaką bowiem interpretację można w takim wypadku nadać powstałej w wyniku obliczeń wartości — przykładowo — 1,73?

Rozważmy dane z tabeli 2.3. Mimo zewnętrznych podobieństw do poprzednich przypadków, są to już dane o charakterze ilościowym, tyle ze zagregowane. Wiek jest zmienną ilościową, można go podać np. z dokładnością do dnia, lub jeszcze większą. Na ogół nie

13