Photo012(2)

s

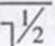
1=1

Przykład 3.2⁴

Niech y₍. oznacza zbiory zbóż w roku /, natomiast jc,. oznacza ilość nawozy

użytych w roku /. Obserwacje dotyczą okresu 20 lat (N=20). Oceny odpowiednich) parametrów są następujące:

P₀ =345, P, =3 , S²e = 662,8,    1

1 ^N

1 = 45,35,    — £(*,- xf= 285,55.    |

^ i=i

Średnie rozkładów a posteriori są równe ocenom uzyskanym za pomocą KMNK tj. £(p„ |y,x) = 345 i E(p, |y,x) = 3.    W

Brzegowe gęstości a posteriori są przedstawione na wykresach nr 3.2, 3.3.

Wykres 3.2. Gęstość a posteriori parametru p₍₎

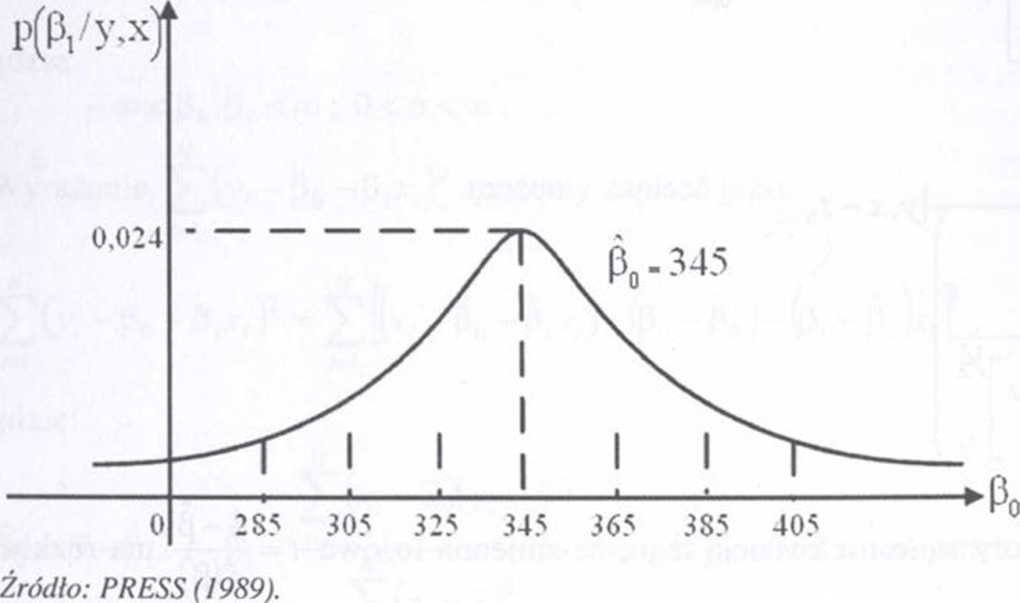
Przykład pochodzi z pracy Press (1989).

Zagadnienia do samodzielnego rozwiązania Zadanie 3.1

A.    Jakie są warunki stosowalności estymatora KMNK? Na czym polega założenie o czystym składniku losowym?

B.    Zapisać funkcję kryterium oraz wyjaśnić istotę estymatora KMNK.

C.    Wymienić i scharakteryzować własności estymatora KMNK.

Zadanie 3.2

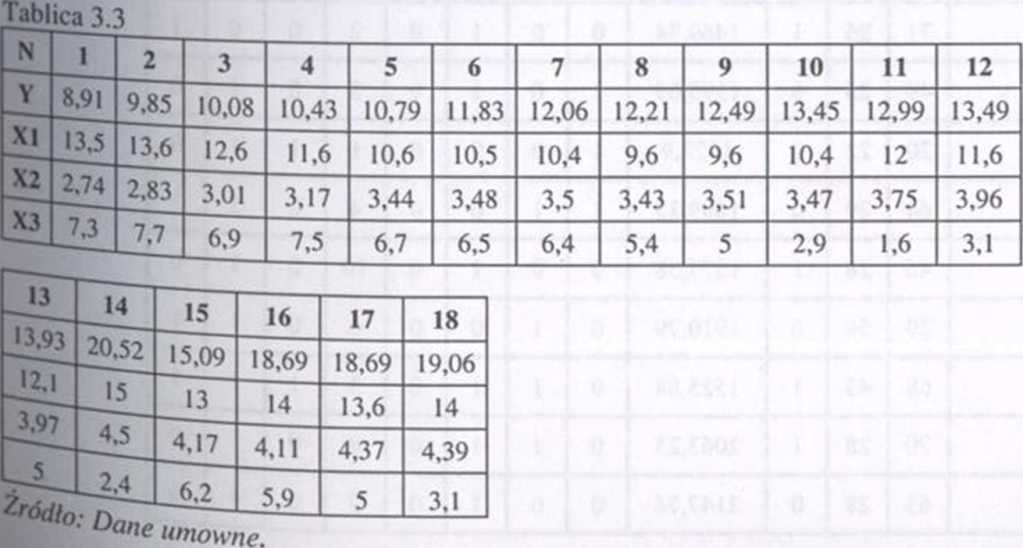
Na podstawie następujących obserwacji (tablica 3.3) oszacować KMNK parametry modelu liniowego zmiennej Y względem zmiennych objaśniających X_UX₂,X₃.

Następnie wyznaczyć standardowy błąd reszt oraz średnie błędy ocen parametrów strukturalnych.