img025

Ale z aksjomatów symetrii i trójkęta (zob. definicję metryki) oraz ze wzorów (2.3), (2.4) otrzymujemy

d(x,x)^ d(x,g) ♦ d(g,J) - d(x,g) + d{x,g)< £ > | - £ .

1 2

dla k,l>n, co oznacza, że cięg x,x,... jest fundamentalny. Twierdzenie odwrotne do twierdzenia 2.2 nie jest prawdziwe.

Przyk ład

Niech dzona odległość

W oznacza zbiór liczb Wymiernych, w którym została wprowe-

głoóć d(x,y) » ix - y I i niech z, »    ⁺    * ••• *

A ⁽ⁱ 10^ł

x iu _1Q-z

» 1,2,...), gdzie oc^ (j*l,2,...) sę cyframi takimi, ze licz

ba z® 0 .atj'toŁg.. •    . jest ułamkiem dziesiętnym nieskończonym i

nieokresowym. Liczba z jest więc niewymierne.

Cięg Zj.Zj,... jest w przestr2«ni (W.d) fundamentalny. Istotnie, dla k<l (k,lcN) mamy

dUk.-jI

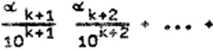
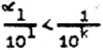
A zetem dla dowolnego £ > 0 wystarczy przyjęć

n - n(e)

0, gdy -l^og c < 0, [-log e],, gdy -loge>0

(funkcje £xj oznacza część całkowity liczby x, tzn. [xj * m, gdzie n<

jest największę liczbę całkowitę spełniajęcę warunek «ś»x), aby dla

wszystkich k > n i l>n (k,lcN) byłe spełnione nierówność d(z_k,z^)<.£.

Zauważmy jednak, że cięg    nie jest zbieżny w zbiorze liczb

wymiernych (dokładniej, w przestrzeni metrycznej (W,d)). Wprawdzie w

przestrzeni metrycznej E. mamy lim z w z, ale z jest liczbę niewy-

¹    n —m

miernę.

Definicja 2.3. Przestrzeń metrycznę (Z,d) nazywamy przestrzenlę zu~ pełń?, jeśli każdy cięg fundamentalny w tej przestrzeni jest zbieżny do pewnego elementu zbioru Z w sensie metryki 6.

Rozważana w ostatnim przykładzie przestrzeń (W,d) nie jest zupełna. Można Jednak udowodnić, że poznane wczeóniej przestrzenie metryczne E_n, Eⁿ i C<«,b> sę zupełne.

Twierdzenie 2,3. Oeśli (Z,d) Jest przestrzenlę zupełnę i 0 i ACZ Jest zbiorem domkniętym w (Z,d), to (A.d) jest również przestrzenlę zupełnę.

Dowód. Ponieważ metrykB d w zbiorze Z indukuje metrykę w dowolnym jego podżbicrze, więc (A,d) jeet przestrzenlę metrycznę. Niech