img055

55

5.1. Metoda uogólnionych wzorców i otoczeń kulistych

Naturalnie, kluczowym problemem staje się przy tym sposób definicji wzorca W\ W najprostszym przypadku wzorzec można utożsamiać z odpowiednim podzbiorem ciągu uczącego (porównaj (19) i (20))

W* = U\    (35)

Reguła decyzyjna oparta na funkcji przynależności (34) sprowadza się wówczas do reguły pokrycia punktów, której zaletą może być w ogólnym przypadku mały procent błędnych rozpoznań. Przy odpowiedniej strukturze przestrzeni cech X (gruba dyskretyzacja wartości cech Xj) liczba decyzji neutralnych i* (braków odpowiedzi - porównaj (13), (14) i (15)) może być zadowalająco mała (rys. 5.2).

A o obiekty ciągu uczącego X obiekt rozpoznawany

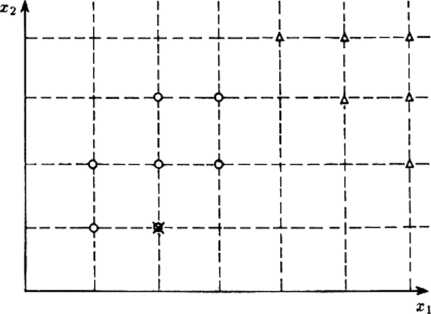
Rys. 5.2. Przy dyskretyzowanych cechach prawdopodobieństwo ropoznania metodą pokrycia punktów jest bardzo duże

Przykład. W zadaniu diagnostyki medycznej często występują cechy przyjmujące tylko kilka wartości: wymioty występują lub nie, gorączka może być silna, słaba lub może wcale nie występować, liczbę chorobotwórczych drobnoustrojów w badaniach mikrobiologicznych oznacza się w skali: