img054

5. METODY WZORCÓW

5*1. Metoda uogólnionych wzorców i otoczeń kulistych

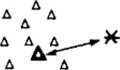
W metodach omawianej grupy odwzorowanie C sprowadza się do określenia zawierania się nieznanego obiektu x w obszarze wzorca i-tej klasy W¹ {W' C X) (rys. 5.1). Funkcję przynależności można tu formalnie zapisać w postaci:

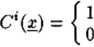
dla x 6 W\ w przeciwnym przypadku.

(34)

X2 ‘ i

X    X

XX XX X

XX    X X

X * XX X XX XXX

A A A A A A

A

XXX

X X

Rys. 5.1. Ilustracja pojęcia wzorca