img068

68
5.4. Zadania drugiej warstwy sieci
5.4 Zadania drugiej warstwy sieci
Sumarycznie pierwsza warstwa sieci może być opisana wzorem
K = 3 (W X)
gdzie W jest macierzą wag, utworzoną z transponowanych wektorów W;- traktowanych jako kolejne wiersze, X jest wektorem normalizowAnyr.h sygnałów wejściowych, a nieliniowy operator S(o) odpowiedzialny jest za wylłór „zwycięskiego” elementu warstwy Kohonena, ustawienie jego sygnału wyjściowego na wartość 1 i wyzerowanie wszystkich innych wyjść.
Warto zauważyć, że w praktycznie stosowanych sieciach klasy CP macierz W daleko odbiega od macierzy kwadratowej, gdyż liczba elementów w warstwie Hohonena przyjmowana jest zwykle jako znacznie większa, niż liczba składowych wektora X. Te liczne elementy warstwy Kohonena mają wydobyć z wejściowego sygnału jego istotne cechy i wybrać stosowny „żeton” (jedyny element t, € K różny od zera), który będzie przekazany do następnej warstwy.
Druga warstwa sieci realizuje algorytm Outstar (Jrossberga. Sygnały wejściowe do tej warstwy tworzą wektor K, a sygnał wyjściowy Y obliczany jest według klasycznej reguły
Y = V K
gdzie macierz współczynników wagowych V składa się z transponowanych wektorów V,-odpowiadających zestawom wag kolejnych neuronów warstwy wyjściowej. Macierz V jest także daleka od kwadratowego kształtu, gdyż z reguły bardzo dużemu wymiarowi wektora K towarzyszy niewielki (porównywalny z wymiarem wektora X) wymiar Y.
Z formalnego punktu widzenia neurony warstwy wyjściowej mają dużo pracy, ponieważ muszą obliczać sumy
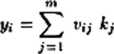
gdzie m ma z reguły dużą wartość. W praktyce jednak jedynie jeden element wektora K ma wartość 1, a pozostałe mają wartość 0 i wystarcza utożsamienie wyjścia y, z pewnym współczynnikiem wagowym tiy. Zauważmy, że to działanie rzeczywiście przypomina odczyt z gotowej tabeli. Na każdym i-tym wyjściu sieci w trakcie procesu uczenia przygotowane zostaje m wariantów odpowiedzi Ody warstwa Kohonena ustali, które z jej licznych wyjść otrzyma „żeton” — na wszystkich wyjściach pojawiają się tylko te wartości v,-j, które odpowiadają numerowi j, dla którego kj = 1.
5.5 Uczenie pierwszej warstwy sieci CP
Aby opisany wyżej schemat postępowania prowadził do sensownych wyników — konieczne jest poprawne ustawienie wszystkich wartości u',j oraz i’ij czyli — realizacja procesu uczenia.
Uczenie sieci CP przebiega równocześnie w obydwu warstwach sieci, ale podczas omawiania wygodnie jest opisać, oddzielnie, jak przebiega proces uczenia w pierwszej warstwie, a jak w drugiej. Uczenie całej sieci CP jest uczeniem z nauczycielem, gdyż ciąg uczący ma formę
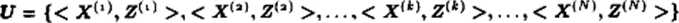
Wyszukiwarka
Podobne podstrony:
IMG202 (2) trudne zadanie, to walka występuje zawsze w pierwszej sekwencji, trudne zadanie zaś —&nbs
Obrazek35 Zadanie 29. (5 pkt) Uczniowie w klasie pierwszej, drugiej i trzeciej wpłacają do banku po
i Urządzenia Mobilne Urządzenia infrastruktury sieciowej o Przełączanie warstwy drugiej OSI 7, o Sie
068 (8) 68 - Zadanie 3»84. W układzie podanym na rys. 3.84 obliczyć wskazanie amperomierza, Jeżeli f
SCAN0006 (68) Zadanie 25. Czynnikiem, który może zdecydować o wzroście popytu na usługi noclegowe w
GrD DEMM Kolokwium nr 1 Zadanie 1. 5 punktów Mamy dwie urny: w pierwszej jest 5 ku
img068 68 68 s 55 * «J5p a.r«sC^hS3Śs8 iaczy szkic nr3 121 <0 <7f*» £<texy «*ic f _
img068 68 Rys. 1.17. Sposób wyz^awzania szerokości widma sygnału tonowej modulacji kata fazowego $M
img068 68 6. Metody aproksymacyjne Naturalnie, podana formula jest niejednoznaczna, gdyż pozwala wyg
IMG068 68 8.9. CIEPŁO SPALA!IA I WARTOŚĆ OPAŁOWA Definicję ciepła spalania i wartości opałowej podan
img068 68 n 3Ś ł fc (h) I < V*~ I h sl —► O. gdy I h I —*■ O i_i j n a to oznac
więcej podobnych podstron