img099

99

Rozdział 8. Sieci pamięci skojarzeniowej

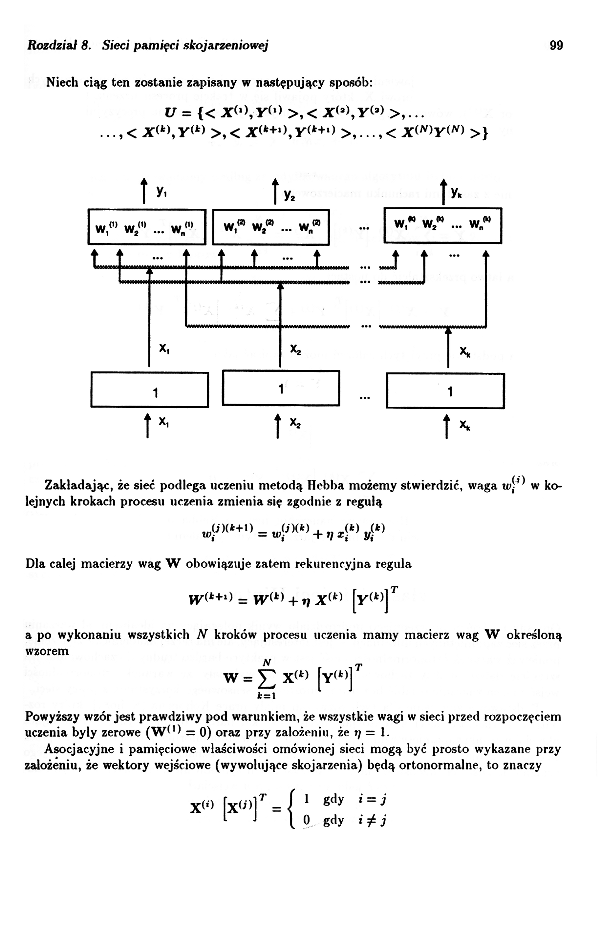
Niech ciąg ten zostanie zapisany w następujący sposób:

u = {<    >,< x<^j),y(^j) >,...

...,< x<*\Y(*> >,< *(*+»), y(*+.)    x(*)y<*) >}

t^y'    t^y»

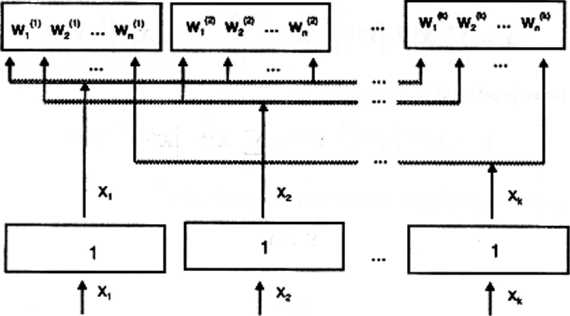
Zakładając, że sieć podlega uczeniu metodą Hebba możemy stwierdzić, waga w-’* w kolejnych krokach procesu uczenia zmienia się zgodnie z regułą

u,P*^+,) = «,^) _{+ ł?z}(*)_y(*)

Dla całej macierzy wag W obowiązuje zatem rek uren cyj na reguła

_W(k+x) _    ₊

x<*> [y“>]

T

a po wykonaniu wszystkich N kroków procesu uczenia mamy macierz wag W określoną wzorem

W = fj X<*> [Y‘^t>]^T

Powyższy wzór jest prawdziwy pod warunkiem, że wszystkie wagi w sieci przed rozpoczęciem uczenia były zerowe (W^(,> = 0) oraz przy założeniu, że tf = 1.

Asocjacyjne i pamięciowe właściwości omówionej sieci mogą być prosto wykazane przy założeniu, że wektory wejściowe (wywołujące skojarzenia) będą ortonormalne, to znaczy

x«> [x«>r=(¹ 8dy ■'=^j

¹ J [ 0 gdy * 3* j