img107

107

Rozdział 8. Sieci pamięci skojarzeniowej

Wynikowa macierz wag ma postać

-1	-1	3
-1	3	-1
3	-1	-1

Mając do dyspozycji gotową wynikową macierz wag (czyli zawartość pamięci sieci BAM) możemy prześledzić, jak sieć działa podczas odtwarzania zapamiętanych informacji. Niech na wejściu sieci pojawi się sygnał 1

X =

-1

-1

Porównanie z ciągiem uczącym ujawnia, że jest to sygnał X^^ł\ który sieć powinna pamiętać. Obliczmy sygnał Y, jaki wygeneruje sieć na swoim wyjściu:

/	■ -1 -ł 3 '		1 '	\ (	' -3 '	\		' -1 '
y = *(ivx) = <i>	-1 3 -1		-1	= *	-3		=	-1
V	3 -1 -1		-1	/ V	5	)		1

Wystarczy rzut oka na ciąg uczący, by się upewnić, że wynik jest poprawny. Otrzymany wektor wynikowy odpowiada dokładnie wektorowi Y^f,>, który w takcie procesu uczenia był kojarzony z podanym na wejście sieci wektorem X = X^^1J.

Sieć poprawnie odtwarza skojarzone informacje w obu kierunkach. Rozważmy przykładowo zachowanie sieci po podaniu na jej wejście Y sygnału odpowiadającego Y = Y⁽¹>.

X - 4>{W^tY) = <1>

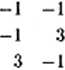
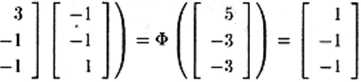
Jak widać, sieć zachowała się poprawnie i odtworzyła na wyjściu X sygnał odpowiadający X = X^<'¹ł. Podobnie można stwierdzić poprawne działanie sieci dla dowolnego z uprzednio zapamiętany cli sygnałów, na przykład dla X = X^f2) sieć poprawnie odtwarza Y = Y⁽²⁾

-1

.3

-1

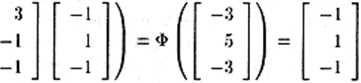
-I

Y = *{WX) = $

-I

3

Podobnych przeliczeń można oczywiście wykonać dowolnie dużo, jest to jednak zbyteczne. Natomiast warto rozważyć zachowanie sieci w przypadku, kiedy podawany do sieci wektor X lub Y nie odpowiada idealnie wektorowi prezentowanemu w trakcie procesu uczenia.

8.5 Działanie sieci BAM przy braku zgodności ze wzorcem

W sytuacji, kiedy podany do sieci BAM sygnał X albo Y nie jest idelanie zgodny z żadnym zapamiętanym wzorcem, sieć poszukuje poprawnej odpowiedzi w sposób iteracyjny. W wyniku tego pojawia się pewien (dłuższy lub krótszy) proces przejściowy i po pewnym czasie