img113

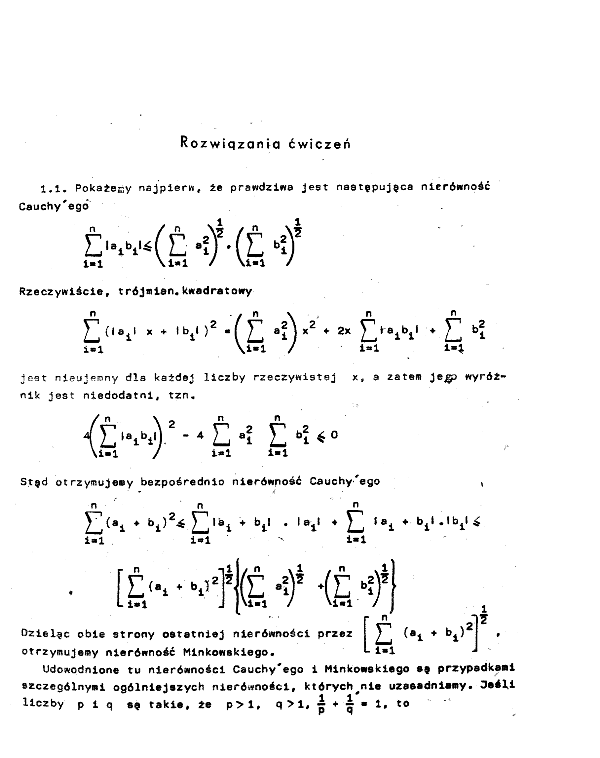
Rozwiqzania ćwiczeń

1,1. PokaZecy najpierw, że prawdziwe Jest nastppujęca nierówność Cauchy'egó

t'w(Ł ‘if-(Ł ■>?]

1-1    \i-i / \i-i /

1

Rzeczywiście, trójmien. kwadratowy

♦²* E^,'^,i^bi^l * £ ^bi

i-i    i-;

E'*v »* ^ibt')² *(L

i-i    \i-i /

jeat nieujenny dla każdej liczby rzeczywistej x, a zatem je#> wyróżnik jest niedodatni, tzn.

t>u°

\i-i /    i-i i-i

Stęd otrzymujemy bezpośrednio nierówność Cauchy-'ego    ,

♦ ^bi)²^C‘®i ^{+ b}i‘ ‘ ^,el‘ ⁴ E ^IOi * ^bi‘-^,bi^l ^

i-1    i-1    >■    1-1

*(5#j

Dzieląc obie strony ostatniej nierówności przez

otrzymujemy nierówność Winkowskiego.

Udowodnione tu nierówności Cauchy'ego i Minkowskiego • * przypadkami

szczególnymi ogólniejszych nierówności, których nie uzaeadniamy. Jeśli

1 1 *

liczby p i q sę takie, że p>l, q>l_# — + ^ • 1, to

L l-l    J