img136

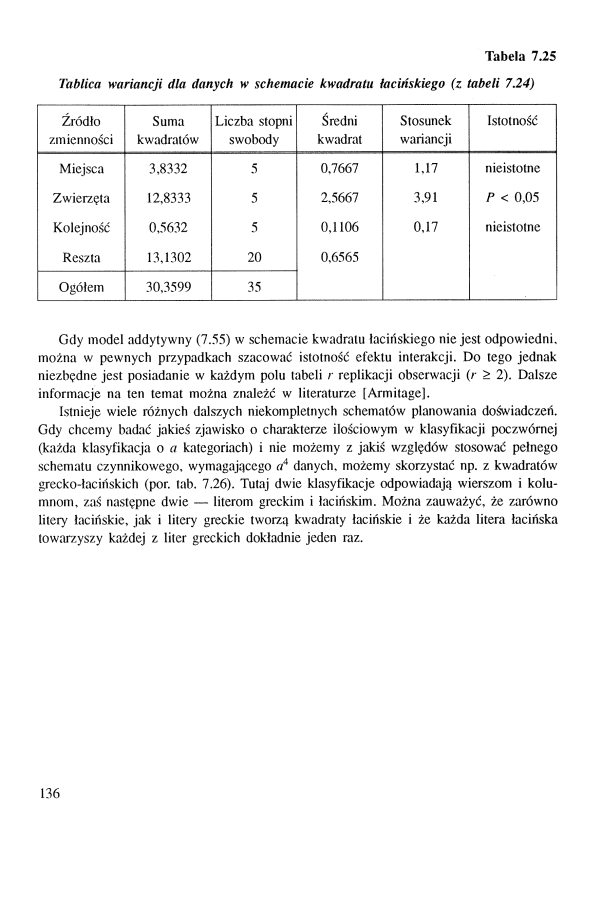
Tabela 7.25

Tablica wariancji dla danych w schemacie kwadratu łacińskiego (z tabeli 7.24)

Źródło zmienności	Suma kwadratów	Liczba stopni swobody	Średni kwadrat	Stosunek wariancji	Istotność
Miejsca	3,8332	5	0.7667	1.17	nieistotne
Zwierzęta	12.8333	5	2,5667	3,91	P < 0,05
Kolejność	0,5632	5	0,1106	0,17	nieistotne
Reszta	13,1302	20	0.6565
Ogółem	30,3599	35

Gdy model addytywny (7.55) w schemacie kwadratu łacińskiego nic jest odpowiedni, można w pewnych przypadkach szacować istotność efektu interakcji. Do tego jednak niezbędne jest posiadanie w każdym polu tabeli / replikacji obserwacji (r > 2). Dalsze informacje na ten temat można znaleźć w literaturze (Armitage).

Istnieje wiele różnych dalszych niekompletnych schematów planowania doświadczeń. Gdy chcemy badać jakieś zjawisko o charakterze ilościowym w klasyfikacji poczwórnej (każda klasyfikacja o a kategoriach) i nie możemy z jakiś względów stosować pełnego schematu czynnikowego, wymagającego a⁴ danych, możemy skorzystać np. z kwadratów grccko-łacińskich (por. lab. 7.26). Tutaj dwie klasyfikacje odpowiadają wierszom i kolumnom, zaś następne dwie — literom greckim i łacińskim. Można zauważyć, że zarówno litery łacińskie, jak i litery greckie tworzą kwadraty łacińskie i że każda litera łacińska towarzyszy każdej z liter greckich dokładnie jeden raz.

136