img�015

2

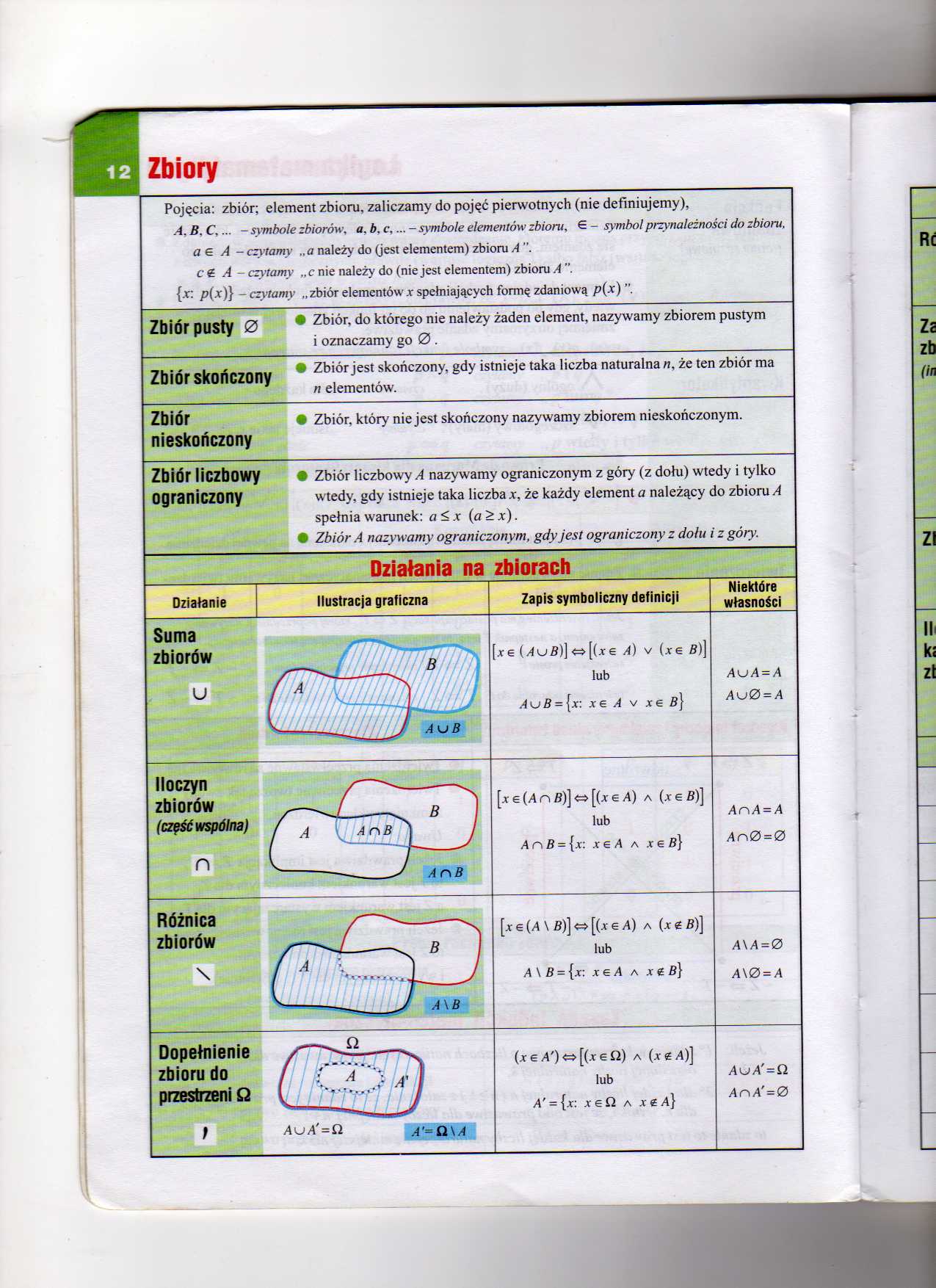
Zbiory

Pojęcia: zbiór; element zbioru, zaliczamy do pojęć pierwotnych (nie definiujemy), A. B. C,... - symbole zbiorów, a. b. c,... - symbole elementów zbioru, € - symbol przynależności do zbioru, a e A - czytamy a należy do (jest elementem) zbioru A ". c £ A - czytamy „c nie należy do (nie jest elementem) zbioru A ". {a: p(x)} - czytamy „zbiór elementówa spełniających formę zdaniową p{x) ”,
Zbiór pUSty 0 * Zbiór, do którego nie należy żaden element, nazywamy zbiorem pustym i oznaczamy go 0 .
7hińr clmńrznnu * Zbiór jest skończony, gdy istnieje taka liczba naturalna «, że ten zbiór ma ^1 n elementów.
Zbiór • Zbiór, który nie jest skończony nazywamy zbiorem nieskończonym. nieskończony
Zbiór liCZbOWy • Zbiór liczbowy A nazywamy ograniczonym z góry (z dołu) wtedy i tylko Ograniczony wtedy, gdy istnieje taka liczba x, że każdy element a należący do zbioru A spełnia warunek: a<x (a>x). • Zbiór A nazywamy ograniczonym, gdy jest ograniczony z dołu i z góry.
Działania na zbiorach
Działanie	ilustracja graficzna		Zapis symboliczny definicji	Niektóre własności
Suma zbiorów u			[ie(/tufi)]»[(j:e A) v (a€ B)] lub ,łufi = {r xg A v xe 5}	AuA = A Akj0 = A
Iloczyn zbiorów (część wspólna) n	^V --------' AnB		[ie(An5)]«[(ie^) a (aeB)] lub A n B = {a: xg A a a e B}	AnA = A An0-0
Różnica zbiorów \			[a e (A \ B)]« [(a g A) a (a e B)] lub A \ B = {a: a e A a a g fi}	A\A = 0 A\0 = A
Dopełnienie zbioru do przestrzeni Q t	AuA'=n A'=Q\A		(a£/4')«[(a6£2) A (Ag/t)] lub A' - {a: a g £Z a x G a}	AnA'=0