skanuj0022(5)

Wprowadza się pojęcie rezystancji obwodu wtórnego odniesionej do obwodu pierwotnego

R'o =

R-

(2.24)

Wtedy

Ł/r₂ = ^/Ó

2¹ 2

(2.25)

Podobnie reaktancja rozproszenia wtórna odniesiona do obwodu pierwotnego

X'r = I I

• a 2

(2.26)

i napięcie na reaktancji rozproszenia wtórnej odniesione do obwodu pierwotnego

a 2^J2

(2.27)

• 2.37 • Co to jest schemat zastępczy transformatora?

Schemat zastępczy transformatora jest to schemat obwodu złożonego z rezystancji i reaktancji dobranych tak, że zjawiska zachodzące w tym układzie odwzorowują z dostatecznym przybliżeniem zjawiska zachodzące w transformatorze. Jednym ze schematów, najczęściej stosowanym, jest schemat zastępczy pokazany na rys. 2.29. Transformator

-^11		Ri	Ii		XŚ2	*2
	Uxi	Uri		do	~*UX2.	Uri
			^Ifr		L		n
Ul		**\\	Ui		Xf	Ui	[
	—	V			r

•2.29* Schemat zastępczy transformatora

o liczbie zwojów N₂, napięciu wtórnym indukowanym U_i2, napięciu wtórnym U₂, prądzie I₂, reaktancji X_a2 i rezystancji R₂ zastępuje się transformatorem o wielkościach wtórnych odniesionych do obwodu pierwotnego, mającym odpowiednio N_x, U'_a2, 1₂, X'_<s2 i #2-

Przy otwartym obwodzie wtórnym (Z'_0(ih = oo) nie płynie prąd w obwodzie wtórnym, a w obwodzie pierwotnym płynie prąd równy prądowi jałowemu I₀. Prąd jałowy I_Q zawiera składową czynną /_ow,

odpowiadającą stratom w rdzeniu P_Fe. Te straty wydzielają się na rezystancji R_Fe schematu zastępczego. Wartość rezystancji R_lv może być wyznaczona z zależności

^Fe —

^Fe

mU\

^7

gdzie m — liczba faz.

Ponieważ U'_i2 = U_n, to można wprowadzić jedno oznaczenie napięcia indukowanego

_U{ = U_n = U[₂

Keaktancja w obwodzie prądu magnesującego może być wyznaczona ze wzoru

Rezystancje R_u R'₂ i reaktancje X_al i X’_c2 mogą być wyznaczone z próby zwarcia transformatora.

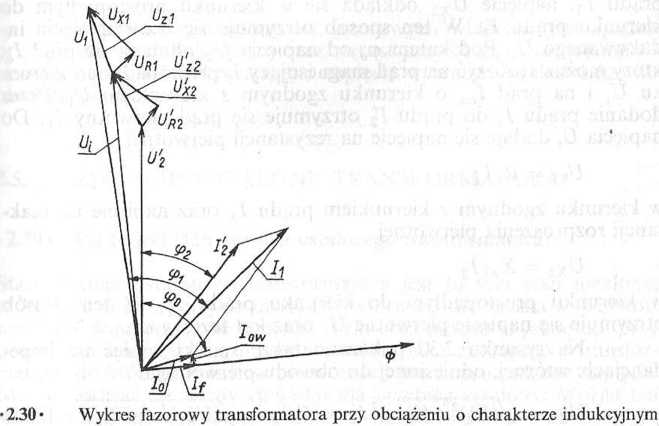
• 2.38 • Jak rysuje się wykres fazorowy transformatora?

Na rysunku 2.30 przedstawiono wykres fazorowy schematu zastępczego transformatora przy obciążeniu o charakterze indukcyjnym. Zjawiska zachodzące w transformatorze przy obciążeniu są dość

47