Obraz0017

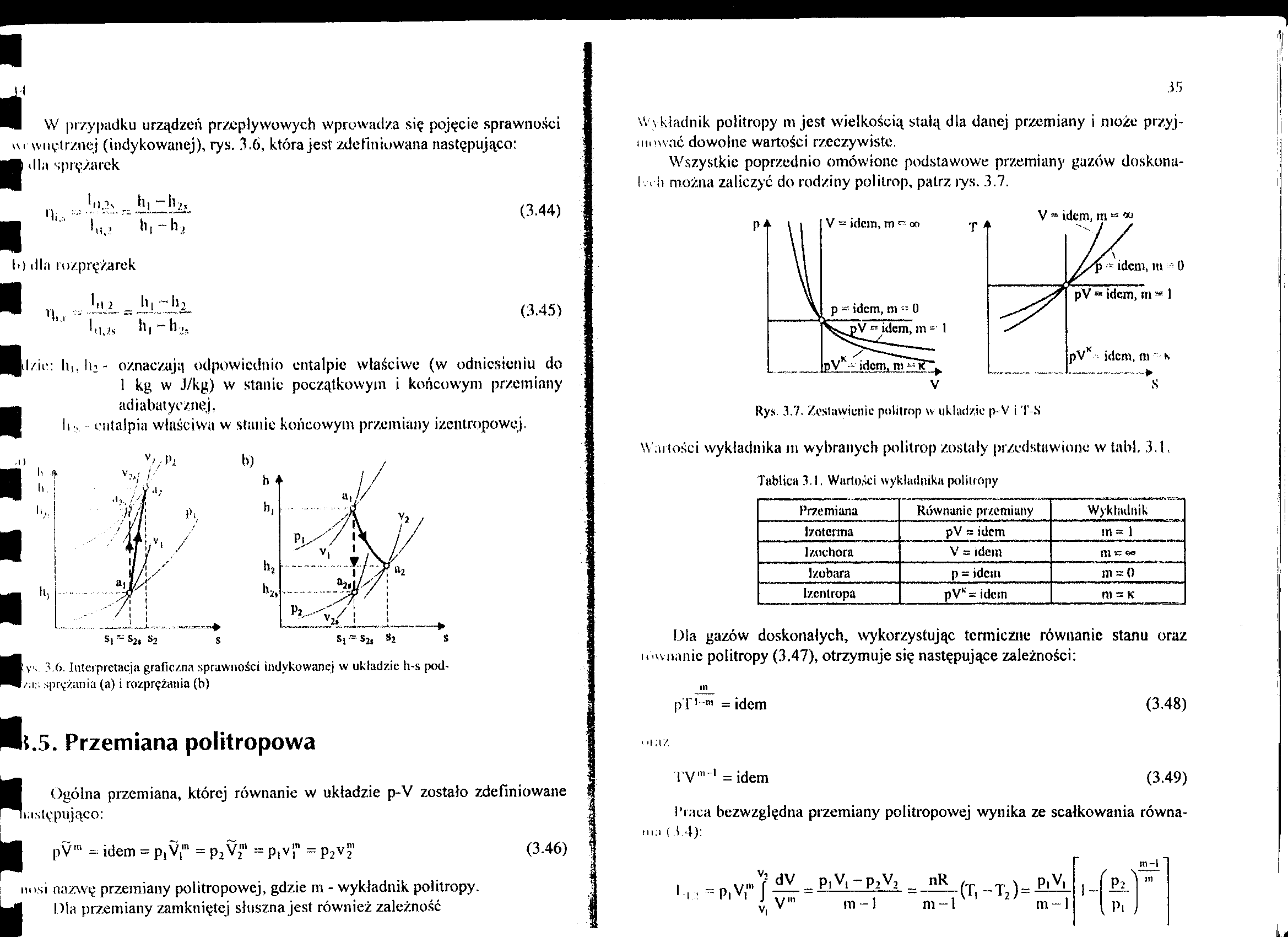
■ W przypadku urządzeń przepływowych wprowadza się pojęcie sprawności wewnętrznej (indykowanej), rys. 3.6, która jest zdefiniowana następująco: i dla sprężarek

(3.44)

(3.45)

, tu.?* .. h, -\r_lf Ki,!

> dla rozpręża rek

l,i ^ _ J][ -1^

l(Us

l/ie:    oznaczają odpowiednio entalpie właściwe (w odniesieniu do

1 kg w J/kg) w stanie początkowym i końcowym przemiany adiabatycznej,

li ,, entalpia właściwa w sianie końcowym przemiany izentropowej.

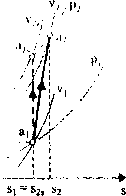
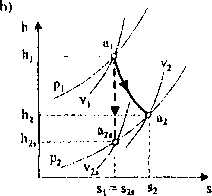
:ys. 3.6. Interpretacja grafie/.na sprawności imiykowanej w układzie h-s pod-/as sprężania (a) i rozprężania (b)

$.5, Przemiana politropowa

Ogólna przemiana, której równanie w układzie p-V zostało zdefiniowane

.istępująco:

(3-46)

P pV^m = idem = _Plvr - p₂vr - p_tvr - p₂v?

nosi nazwę przemiany połitropowej, gdzie m - wykładnik politropy. Ld| Dla przemiany zamkniętej słuszna jest również zależność

Wykładnik poiitropy ni jest wielkością stałą dla danej przemiany i może przyjmować dowolne wartości rzeczywiste.

Wszystkie poprzednio omówione podstawowe przemiany guzów doskonu-Iwh można zaliczyć do rodziny politrop, patrz rys. 3.7.

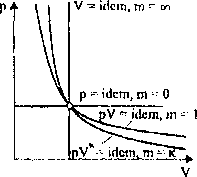
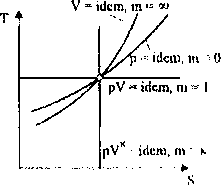
Rys. 3.7. Zestawienie politrop w u kładzie p-V i T-S Wartości wykładnika m wybranych politrop zostały przedstawione w tahk 3,1,

Tablica 3.1, Wartości wykładnika poiitropy

Przemiana	Równanie przemiany	Wykładnik
Izoterma	pV s= idem	m = i
Izochora	V a idem	m *=
Jzobara	p = idem	m ~ 0
I/.cnlropa	pV^k - idem	m = k

Dla gazów doskonałych, wykorzystując termiczne równanie stanu oraz równanie poiitropy (3.47), otrzymuje się następujące zależności:

m

pTi m = idem	(3.48)
ł V'^n 1 = idem	(3.49)

iTaoa bezwzględna przemiany politropowej wynika ze scałkowania równani, i (3.4):

I

_Vm ?dV PlVl-P2V2 _ nR ¹ ' i. V'ⁿ m -1

m -1

m -1

(T,-T₂) =

P,V|

m -1