m19

•A

w

.-.■ ii':-

m-m-:

m

■nj

ŁfA'

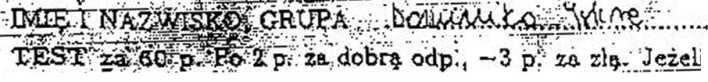
ijzdąnie jest prawdziwe, to postaw

krzyżyk wpierwśzejr kólumnię,: Jeżeli fałszywe, w drugiej. Można nie stawiać pewnych, krzyżykó

p f. • - -.........^: ■    ^r '

1.    Dowolne dwie macierze p0siaxb.j5.ee równe ilości wierszy można pomnożyć.

2.    Jeżeli do pewnego'wiersza dodamy'jedynki, to wartość wyznacznika, nie zmieni "się.

3.. Jeżeli macierz ma więcej kolumn niż wierszy, to nie istnieje wyznacznik z tej macierzy

4.    Rząd każdej macierzy nie przekracza ilości jej wierszy.

5.    Układ równan z —y ~Śz = 0, —1 + y■« 2 jest sprzeczny,

[6. Pewne układy równań mogą. być jednocześnie sprzeczne i nieoznaczone,    Tć”-*—

77^sńed2inę-toikeji In| cóa |j- jcafr-ft;- —-^--—

8.    Funkcja arcsin(xcos2x) jest nieparzysta.    ' >

9.    Fdnkcja |arcctgzj jest parzysta.-:

10.    Funkcje arę tg² a: oraz _v/tg~5¹ są oćłwrdtno.

11.    Funkcja f(x) =» z — yx jest- różnowartościowa.    *    .......

12.    Funkcja y/l~ § jest malejąca. :;;-    |    . .    . i •    *

13.    Funkcja £ 4- arccos x przyjmuje: tylko wartości dodatnie.    -    -

14.    Prosta plonowanie może przędąc;wykresu funkcji w trzech punktach.

15.    Jeżeli funkcja jest rosnąca,: to iestóróznowartościowa.

Zawsze jeżeli skończone granica dwóch funkcji    granica ich ilorazu^.---

17. Jeżeli funkcja jest różniczkowalna w pewnym pi^^i^tojestona ciągła w u^-pMtcie. ^—lS. Wyrażenie 0 — 0 jest wyrażeniem nieoznaczonym.    „

■ ,    Pochodna funkcji rosnącej jesłrzawsżerfunkćją rosnącą.

20.    Jeżeli granice jednostronne /(x) w puhkcie *• są ró^-zi*, to /{z) jest ciągła -,v u.

21.    Jeżeli f^f(z) istnieje, to jest tangćusehTńachylenia',siecznej do wykresu w punkcie (s_r/'(.r.

22. Funkcja /(x) = 3x ~ sin ^ jest rosnąca w zbiorze R.    "    -.-4—

23.    Funkcja/(x) = | In żj ma minimum, lokalne.

24. Funkcja f(x) ~ Xyfx jest wypukła.dla każdego x > 0.    .4    .i

3£. Maksimum lokalne może wystąpić, także w punkcie, w którym nie istnieje pochodna.

26.    Funkcja f(z) = 4— ma asymptotą poziomą.

27.    Asymptota ukośna prawa, to prosta ' y = mi -r n, o ile lim [/(z) — mi — n] = 0,

Iloczyn dwóch ułamków prostych pierwszego rodzaju jest zawsze ułamkiem prostym.

29.    Całka, nieoznaczona nigdy nie jest¹ funkcją stalą,

30.    Wyrażenie    jcst-ulamkiem prostym.    .....

31.    Równanie parametryczne z = l —2f, y = 3 opisuje pewną linią prostą.

'_32. Krzywa o Hiiur — 2łny> (we wsp. biegunowych) jest określona dla wszelkich dodatnie:

(33. Funkcja f{x) = x²^ jest całkowalna w przedziale (—1, Ij.'

[34. Sensem geometrycznym całki oznaczonej jest pole figury schodkowej.

35. Jeżeli całka niewłaściwa daje się nWliczyr , to    —.. ■—:—_-

fz⁴c^x/*dz> 0.

l    •    _<    .

Na odwrocie u góry należy odpowiedzieć na PYTANIE za 15 p._t zaś w dolnej połowie.^ rozwiązać ZADANIE za 25 p.. Pytanie i zadanie są na tablicy,    - yj;

Na ¹⁵trójkę” trzeba zdobyć rcunimwn-50 p. Każde dodatkowe 10 p. podwyższa ocenę o 0,