Matura z matmy arkuszK

Arkusz VI

m

Zadanie 9.

Rzucamy dwa razy sześcienną kostką do gry. Prawdopodobieństwo, że za drugim razem wypadnie liczba oczek podzielna przez 3 jest:

1 11 1

A. mniejsze od - B. większe od- C. równe-    D. równe —

m

Zadanie 10.

Graniastosłup ma 96 krawędzi. Liczba wierzchołków tego graniastosłupa wynosi: A. 32    B. 64    C. 96    D. 48

Zadanie 11.    l p.

Do okręgu o środku w punkcie S = (-1,4) i promieniu r = V3 należy punkt:

A. A = (V3-1,4)    B. B = (0,2)    C C = (-l,l) D. D = (l,3)

Zadanie 12.    1 p.

Liczba 3 log ₁ 8 -log₃ 27 jest równa:

A. 6

B. 9

C. -12

D. -6

Zadanie 13.    1P-

Która z podanych funkcji nie przyjmuje wartości ujemnych?

A. y=*25+4 B. y«i*-3*+2 C. y=^łj    D-    ■

Zadanie 14.    ifeffe

Jeśli liczba 2 jest pierwiastkiem wielomianu W£t) =x³ -5x² +p^x + 20/^to V    równe:

A. 4

B. -4

C. 2

D. -2

Zadanie 15.

lp.

Trójkąt równoboczny o boku długości 4 cm obrócono wokół prostej zawierającej wysokość trójkąta. Objętość powstałej bryły równa jest:

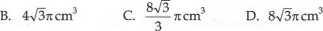
lp.

Poziom podstawowy

A. 14,5 cm³

Zadanie 16.

O pewnym trójkącie wiemy, że jeden z jego boków ma długość 10 cm, a promień okręgu opisanego na tym trójkącie ma długość równą 5 cm. Trójkąt ten jest

A.    ostrokątny

B.    prostokątny

C.    rozwartokątny

D.    nie można na podstawie tych danych rozstrzygnąć, czy jest ostrokątny, prostokątny czy rozwartokątny

Zadanie 17.    lp.

Dana jest funkcja /(z) =2x^z -3z+4, z eR. Zbiorem rozwiązań nierówności /(z) <4 jest:

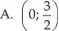
B. (1; 2)

D, (0;i)

lp.

Zadanie 18.

Koło ma średnicę o długości 6 cm. Jeśli długość promienia tego koła zwiększymy o 2 cm, to pole koła wzrośnie o:

A. 33 i % 3

B. około 178%

C. 133—% 3

D. 144%