Mechanika ogolna0014

29

28

rad

....... = 2 • co_n

Dane:

P - ciężar [N],

k - te w. współczynnik sprężystości sprę-

"N"

zyny

n-n

co, = const. =-= co

30

-długość sprężynynieobciążonej [m].

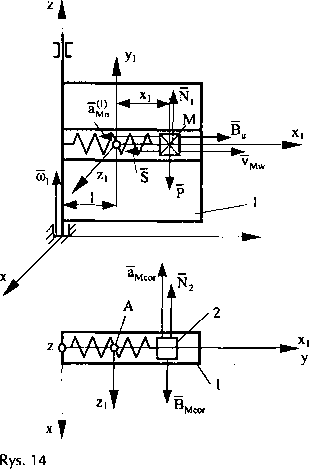
Na rysunku 14 widzimy, że bryła 1 obraca się wokół nieruchomej osi z, ruch tej bryły to ruch unoszenia dla bryły 2. Bryła 2 się przemieszcza, czyli punkt M porusza się względem bryły 1. Przyjmujemy układ osi xyz. Punkt A, który jest początkiem ruchomego układu odniesienia Xiy!Z! związanego z bryłą 1, wiążemy z końcem sprężyny o długości początkowej 1 (zakładamy, że ruch punktu M odbywa się od punktu A). Określimy siły zewnętrzne działające na punkt materialny M:

N[ - reakcja podłoża na kierunku osi z układu odniesienia,

N₂ - reakcja podłoża na kierunku osi x,

S = k ■ A - wartość siły reakcji sprężyny, gdzie A - deformacja sprężyny,

B_u = -m • a_u - siła unoszenia.

W naszym przypadku deformacja jest równa przemieszczeniu liniowemu punktu M, czyli A = xi. Przyspieszenie unoszenia punktu M jest lo przyspieszenie liniowe punktu M przypisanego bryle 1. Ponieważ brylu 1 jod w mchu (linolowym, przyspieszenie to można rozłożyć na dwie składowe lUMHWllie i Nlycznc:

-a<‘) -aW ₊o(')

^,lMu “ ^dM ~ “Mn ^T “Mi’

ule ei, = const., czyli = 0. Ostatecznie więc przyspieszenie unoszenia wynosi:

^a Mu “ ^aMn ⁼ ®i 0 ^{+ x}')’

Ktd/ir I + xi - odległość punktu M od osi obrotu bryły 1. Wiiilość siły unoszenia wynosi zatem:

p

ll„ =- m • a_Mu = m • a$_n = —cof (1 + Xj),

I ł_{t t)i} = -m • a_Mcor - siła Coriolisa.

|*i zyspicszenie Coriolisa wyznaczamy ze wzoru:

W naszym przypadku <o_u =    , a prędkość względna punktu M v_Mw = x,. Wek-

łni przyspieszenia Coriolisa a_Mcor jest równoległy do osi x niemchomego układu odniesienia, a jego zwrot przeciwny do zwrotu tej osi. Wartość tego wektora wynosi:

Wsin- = 2co₁-x₁.

/yisinic z wcześniejszym wzorem wektor siły Coriolisa B_Mcor ma kierunek pi zyspieszenia a_Mcor, jego zwrot jest przeciwny do zwrotu wektora przyspieszeniu, czyli zgodny z osią x nieruchomego układu odniesienia. Wartość tego wek-li u u wynosi:

m-a_Mcor=2-co-x,.

Mńwnaniu    różniczkowe    ruchu względnego masy M

•    na    kierunku osi    xp    ni • x,_M    = -S + B_u,

•    na    kierunku osi    yp    m • y,_M    0 P i    N,,    bo    y_1M    ^ consl.,

•    na    kierunku oni    zp    ni ż_IM    - 0 - ■ N,    ł H,,,,,    bo    z_IM    -■ consl.