Mechanika ogolna0033

()()

i.3. Ruch płaski bryły

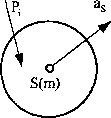
l^>;imiętamy z kinematyki, że ruch płaski to ruch, jaki wykonuje bryła w jednej płaszczyźnie, będący złożeniem ruchu postępowego i ruchu obrotowego. Ruch obrotowy bryły najlepiej jest opisać jako obrót względem punktu, dla którego biegunowy moment bezwładności jest najmniejszy. Takim punktem dla bryły jesl środek masy (rys. 34). Wiemy też, że środek masy przemieszcza się w czasie. Różniczkowe równania ruchu płaskiego bryły będą następujące:

n

^m-*s=2X

i=l

n

^m-y_s=Z^piy

i=l

n

i=l

(127)

y

o

(>

X

Rys. 34

1’icrwsze dwa równania wzoru (127) opisują ruch postępowy bryły, trzecie równanie zaś ruch obrotowy bryły względem środka masy.

Przykład 10

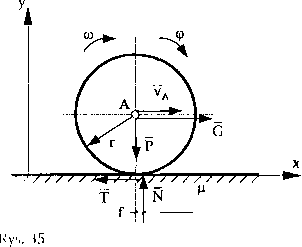
K rążek toczy się bez poślizgu po chropowatej równi pod wpływem przyłożonej slalcj siły G (rys. 35). Opisać zjawisko ruchu krążka, jeśli podczas ruchu pozostaje on w płaszczyźnie rysunku. Zakładamy, że równia jest sprężyście odkształ-ealna.

< tkreślimy wszystkie siły działające na krążek. Zakładając, że punkt A jest środkiem masy krążka, w punkcie tym zaczepiamy siłę ciężkości P d/,inlaji|c;| na kr;|żek oraz silę G wymuszającą ruch krążka. Środek masy krążku będzie poruszał się zgodnie ze zwrotem i kierunkiem siły G. Równin JonI t'lun|uivvala i od-kszlalealna Niiiężyśeie, reakcja normalna jest przesunięla UH (♦IHIliMtlłl względem

Arnilka masy o f w stronę założonego ruchu. Siła tarcia T ma zwrot przeciwny do założonego kierunku ruchu. Przyjmujemy układ odniesienia zorientowany Ink, że oś x ma zwrot zgodny z kierunkiem ruchu, a oś y jest prostopadła do iiirlui. Równanie opisujące ruch środka masy na kierunku osi x układu odnie-Hinuii ma postać:

m • x_A = G -T .

Dane:

G - siła wywołująca ruch [N],

P - siła ciężkości działająca na krążek [N], p - współczynnik tarcia suchego, f- współczynnik tarcia tocznego [m], r - promień krążka [m].

Nu kierunku osi y nie występuje ruch środka masy, stąd: m ■ y_A = 0 = N-P .

/ ińwnania tego znajdziemy: N = P. Równanie opisujące ruch obrotowy krążka w/ulętlem środka masy będzie następujące:

I_A -ćp = T-r-N-f.

hmkl (' jest chwilowym środkiem obrotu bryły. Wykorzystując zależności ki-i ir u i.i i yczne, napiszemy:

v_A-r-co,

i-/yli.

*A	- r • (p,
	r • <p,
^XA	r • <p.