Mechanika ogolna0002

(.5.

(.5.

^RlH

3-5-1

3.5.5

3-5.3

obrotowy bryły wokół nieruchomego punktu (ruch kulisty)....    77

Opis mchu kulistego bryły ........................................................... 77

Uproszczona teoria ruchu kulistego............................................... 82

,, p ■ Ruch bąka symetrycznego............................................................ 87

dowolny bryły .......................................................................... 92

^f¹?¹°V ENERGETYCZNE opisu zjawiska RUCHU ................. 93

4.1. tne*. ■ ,

41-1

4-1-2

4.1.3

gia kinetyczna ............................................................................. 93

Energia kinetyczna punktu materialnego ....................................... 93

Energia kinetyczna bryły .............................................................. 94

4 2 Pra ^^nerg*^a kinetyczna układu brył..................................................... 98

4 2    skonana przez układ sił ........................................................ 100

^ 2 ^ł - Praca elementarna i całkowita wykonana przez siłę i układ sił......... 100

4.2.3

4.2. <i

4.2.5

4.2.6

4.2. >

Praca elementarna wykonana przez siły działające na bryłę ............ 102

Praca sił wewnętrznych................................................................ 107

Zasada równowartości energii kinetycznej i pracy.......................... 110

- Moc układu................................................................................. 116

Pole potencjalne sił .................................................................... 116

Zasada zachowania energii mechanicznej ...................................... 125

^Zas ^^{IKĄ ANAL,TYCZNA} ......................................................... ¹³¹

' ^ * ^-tla prac przygotowanych (wirtualnych) ..................................... 131

5.1.2

Praca, przygotowana .................................................................... 131

Praca przygotowana układu sił działających na bryłę w mchu

5.1.3

postępowym ............................................................................... 133

Praca przygotowana układu sił działających na bryłę w mchu

5.1.4

obrotowym ................................................................................. 134

Praca przygotowana układu sił działających na bryłę w mchu

5.1.5

płaskim ................ 134

Praca przygotowana układu sił działających na układ brył

Zasa,

(np. mechanizm) ......................................................................... 135

tia ró>vnowagi kinetostatycznej...................... 145

h    ró-wnanie dynamiki ............................................................... 149

I. Równania Lagrange’a.................................................. 154

5-4. „    Więzy i ich równania..................................... 154

5.4.2^    Wspcółrzędneuogólnione.............................................................. 158

5.4.3^    Uogólnione przesunięcie wirtualne ............................................... 161

5.4.4^    siły uogólnione........................................................................... 162

5.4.5^    Rówmowaga układu..................................................................... 167

5.4.6„    p_Qj_e p₀t_encj_ai_ne.......................................................................... 168

■>.4.8,

5.4.9,

5.4.7,    Rówmowaga statyczna w polu polcncjnliiym.................................. 170

Rówmowaga Lagrange’a drugiego lod/iiju ..................................... 171

Inna wersja równań Lagrangói (lnigirgo rodzaju ..................... 1/8

IKATUR^......................................................................................... (Hi

WSTĘP

Dynamika to część mechaniki, która zajmuje się ruchem ciał i przyczynami powodującymi ten ruch. Tradycyjnie dynamikę dzielimy na następujące części:

•    dynamikę punktu materialnego,

•    dynamikę układu punktów materialnych.

Punkt materialny to najprostszy model ciała stałego. Mówimy na przykład o ruchu punktu M jako ustroju bezwymiarowym, któremu przypisano masę m (rys. 1).

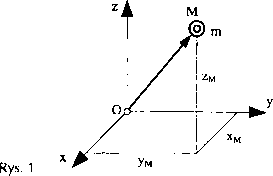
i'_M = r_M(t) jest to wektor promień, a w postaci analitycznej zapisujemy go jako: ^,?M ^{= x}M^,i+y_M-j^+zM^,k-

Zasady dynamiki

W rozważań i a di przyjmujemy za podstawę zasady mechaniki klasycznej sformułowane przez Newtona. Zasady te zostały określone przy następujących założeniach: ruch punktu, którego masa jest siata, odbywa się względem nieruchomego układu odniesienia, a pomiar czasu rudni jest pomiarem czasu absolutnego (bezwzględnego).