Mechanika ogolna0051

Wielkość okieślomi juko eiillui ki/ywol|n|uWM % pracy elemeiiliimej;

L_ab = J 8.L -1(P_x -clx I P_y -dy l I’, (I/,) } l*_x -dx I | P_y -dy I ) \\ cl/

(AB)    (I    0    (I

(IM)

nazywamy pracą całkowitą wykonaną przez siłę P. Pracę całkowitą można również zapisać jako:

L = j8L = |(P_X ■ x + P_y ■ y + P_z ■ ż)dt    (165)

o

Jednostką pracy w układzie SI jest [N-m].

Uwaga!

Jeżeli w układzie występuje układ sił działających na punkt, czyli:

i⁵ = 2^.

i=l

to wówczas praca elementarna wykonana przez układ sił jest algebraiczną sumą prac elementarnych wykonanych przez poszczególne siły:

5L = j^5L_;    (166)

i=l

Analogicznie praca całkowita wykonana przez układ sił jest sumą algebraiczną prac całkowitych wykonanych przez poszczególne siły:

L = f_jL_i    (167)

i=l

4.2.2. Praca elementarna wykonana przez siły działające na bryłę Ruch postępowy bryły (rys. 56)

Załóżmy, że na ciało pozostające w ruchu postępowym działa układ sił zewnętrznych P,,Pj...P_n. Przy postępowym ruchu ciała trajektorie wszystkich jego punktów są krzywymi przystającymi. Wektory elementarnych przemieszczeń wszystkich punktów ciała są geometrycznie równe:

d? = dij = di^.

W przypadku prędkości jest lak sumo, HniuMittiiiiH praca układu sil jest wu,* lówuu:

«l - - Ż«Li - ŻPi ’ vj • dt = £P, •'v_s • dt = d| • ^Pi ■

il    i=l    i=l    i=l

()/,linczując przez P wektor główny sił zewnętrznych, d% — wektor elcmeiilm ncgo przesunięcia środka masy, mamy:

(KiH¹

8li^p,=P-d%

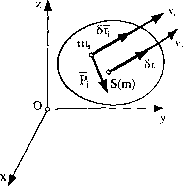
Rys. 56

Ruch obrotowy bryły (rys. 57)

Obliczmy pracę elementarną wykonaną przez układ sił P^Ę... P_n przyłożony d" bryły w ruchu obrotowym.

Praca elementarna jest równa:

5L = £SLj =]£P_rv<!t,

i=l    i=l

gdzie V; - prędkość liniowa i-tego punktu.

W ruchu obrotowymi prędkość liniowa i-tego punktu jest równa:

praca elementarna będzie więc określona jako:

8L = ^o5^xPj)dt.