Mechanika ogolna0055

I. |BI.= J(M-P,.f)-A,

o    ^r

ostatecznie praca całkowita to:

L_AB=(M-P,-f)^.

M_A <li|i-( N I' I I i M )il«|.

WnIiiwiii|i|i‘ te wiclkońci do wzoru mii pilicę, oli /yiiiiiuiy ol!^pl) T-dr_A l (M -1* - f -T-r)d<p.

Wiemy, że: dtp --¹—, r

użyli: 8L--T-dr_A +(M -P, f-T

r

dr

po uproszczeniu: 8L = (M-Pj - f)——.

r

Praca całkowita wykonana przez układ sił będzie równa: ^Sa    dr.

4.2.4. Zasada równowartości energii kinetycznej i pracy

Niech na punkt materialny o masie m działa siła P (rys. 64).

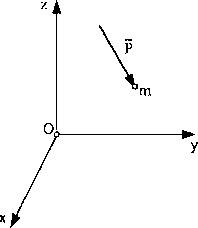
Rys. 64

Dynamiczne równania ruchu punktu względem przyjętego układu odniesienia będą mieć postać:

m ■ x = P_x m • y = P_y m ż = P,

:*!-i ■■■ i■ ■■..    : i...... ■ ■ J    ■    '■ ¹' ■■■ '"i"»i’¹ W¹ "tP":¹ 'HWłi/ ' ■ ''JBiPMI,...........i.........V'":l'■ Yi-"¹'^5,!i" iii.i

1'oiiiiiu/yiiiy równniiin (17) przez prędkości o odpowleduinli klmmluicli i U* rówiiiimn dodamy do siebie stronami, wówczas otrzymamy;

m(x • x + y • y + ż • ż) = P_x • x + P_y • y + P_z • ż.

Wyrażenie po lewej stronie jest pochodną energii kinetycznej po czasie (zależność (152)):

dE    •    /

dt

■— = m(x-x-t-y-y + ż-ż) = E,    j

czyli:

dE = (P_x • x + P_y • y + P₂ ■ żjdt, gdzie:

8L = (P_x ■ x + P_y • y + P_z ■ ż) dt.

Ostatecznie możemy zapisać:

dE = 8L    (176)

Z równania (176) wynika, że elementarna energia kinetyczna jest równa elementarnej pracy. Jeżeli równanie (176) obustronnie scałkujemy, to dostaniemy:

JdE = j 8L,

co po rozwiązaniu całki da nam:

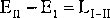
(177)

Równanie (177) to tzw. zasada równowartości energii kinetycznej i pracy. Określa ona, że przyrost energii kinetycznej układu między dwoma charakterystycznymi położeniami (I, II) jest równy pracy całkowitej wykonanej przez wszystkie siły, w czasie gdy przyrost ten następuje. Zasadę tę można stosować zawsze do opisu zjawiska ruchu punktu, bryły czy układu brył.

Jeżeli: L_M1 = 0, to: E_n - Ej = 0.

E_n = E, = const.

Zależność (178) to tzw. zasada zachowania energii kinetycznej.

(178)