Mechanika ogolna0086

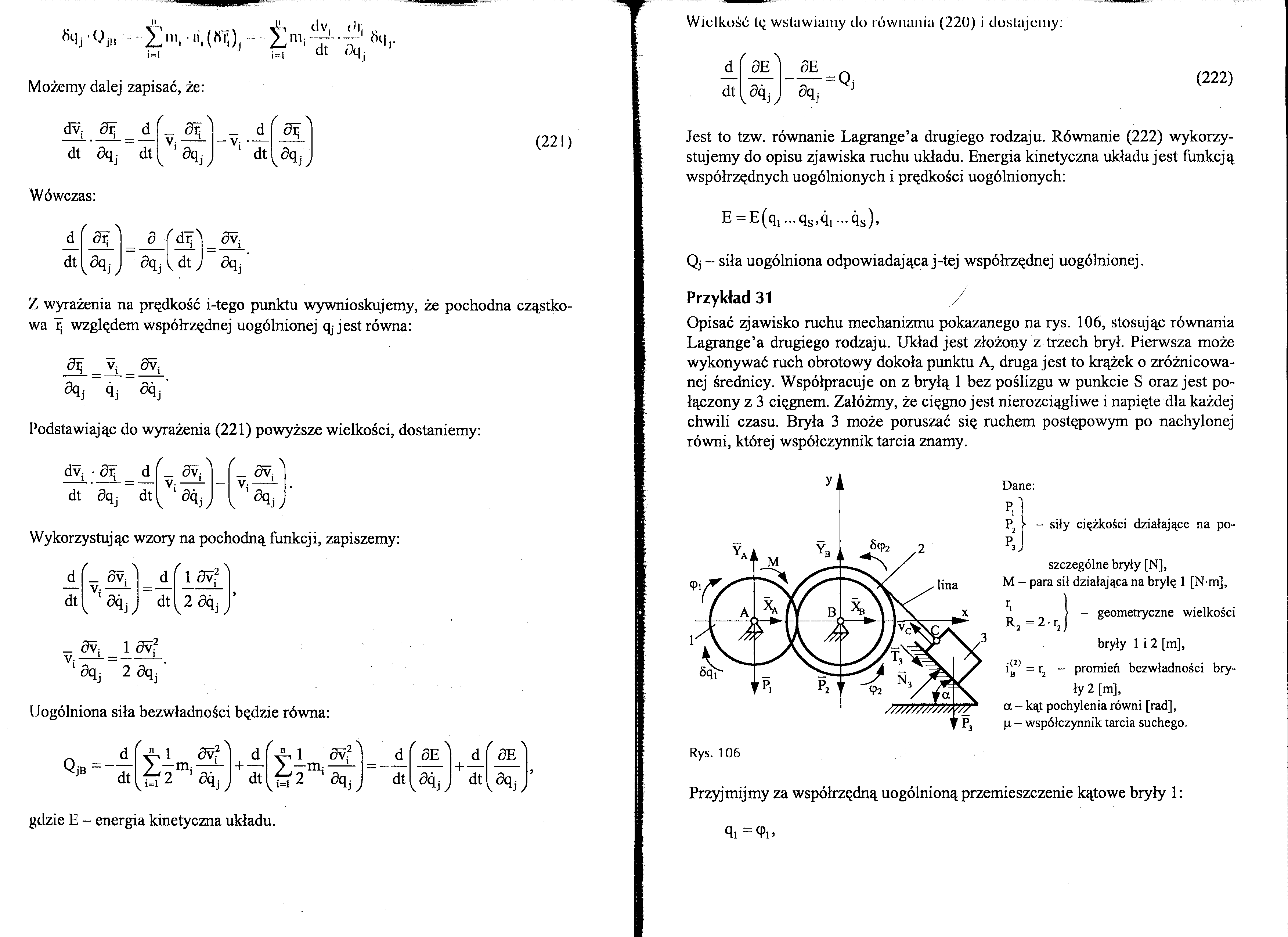
(221)

1>'. a (*>;), ilⁿ\ «H

Możemy dalej zapisać, że:

dVj dr_{ _ d dt 9qj dt

	_ d	(<%)
^vir- l ^5c*iJ	- V:-- dt

Wówczas: 8 (dłp. oy,

v^5qj;

dą_s l dt J aąj

/ wyrażenia na prędkość i-tego punktu wywnioskujemy, że pochodna cząstkowa "ij względem współrzędnej uogólnionej qj jest równa:

9qj <łj 9ą_j

Podstawiając do wyrażenia (221) powyższe wielkości, dostaniemy:

d	f >
dt	^vi—^L l ^dchj		^vi

Wykorzystując wzory na pochodną funkcji, zapiszemy:

	_ d
	dt

_d dt

_ dVj    1 dvf

^V‘ 9qj    2 5qj

Uogólniona siła bezwładności będzie równa:

QjB ~

dt

tf2

+- Ż”^m.—

dt!-fc-2 ‘8q,

,_d_f _3E

^dtl^5<łj.

8E

dt

gdzie E - energia kinetyczna układu.

d
dt	1^1 ż

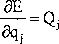
Jest to tzw. równanie Lagrange’a drugiego rodzaju. Równanie (222) wykorzystujemy do opisu zjawiska ruchu układu. Energia kinetyczna układu jest funkcją współrzędnych uogólnionych i prędkości uogólnionych:

E = E(q₁...q_s,q_I...q_s),

Qj - siła uogólniona odpowiadająca j-tej współrzędnej uogólnionej.

Przykład 31    /

Opisać zjawisko ruchu mechanizmu pokazanego na rys. 106, stosując równania Lagrange’a drugiego rodzaju. Układ jest złożony z trzech brył. Pierwsza może wykonywać ruch obrotowy dokoła punktu A, druga jest to krążek o zróżnicowanej średnicy. Współpracuje on z bryłą 1 bez poślizgu w punkcie S oraz jest połączony z 3 cięgnem. Załóżmy, że cięgno jest nierozciągliwe i napięte dla każdej chwili czasu. Bryła 3 może poruszać się ruchem postępowym po nachylonej równi, której współczynnik tarcia znamy.

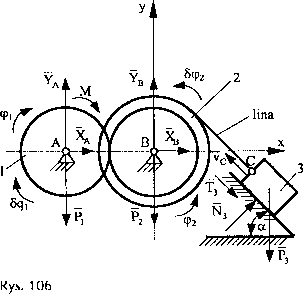
Dane:

^P,1

P₂ ) - siły ciężkości działające na po-

^P3J

szczególne bryły [N],

M - para sił działająca na bryłę    1    [N-m],

r    )

'    1    —    geometryczne    wielkości

R₂ =    2 • r₂ j

bryły 1 i 2 [m],

ig'’ = r₂ - promień bezwładności bryły 2 [m],

a - kąt pochylenia równi [rad], p - współczynnik tarcia suchego.

Przyjmijmy za współrzędną uogólnioną przemieszczenie kątowe bryły 1:

=<fc,