P1010602

96 i j Drgania swobodne

------ I

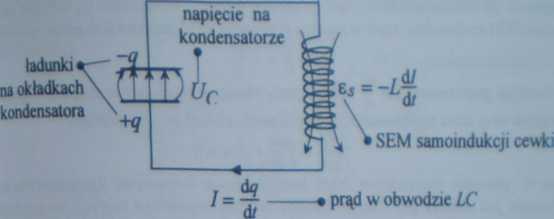
■ Równanie drgań w obwodzie LC otrzymujemy z II prawa Kirchhoffa, k_tó mówi, że suma spadków napięć w obwodzie równa jest sumie sil eleldromotoryc nych w tym obwodzie. W naszym przypadku, przy braku oporu R w obwodzi I

____j.___________■___.______ _    a    I

mamy do czynienia jedynie z napięciem na kondensatorze \Ję - ~ i z SHM I

ĄJ    C    1

samoindukcji cewki z₃ =    Przedstawmy 0 prawa Kirchhoffa w postaci

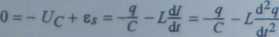
Dzieląc obustronnie powyższe równanie przez (-L) mamy

%₊₇W=o

dt² LC

Jest to, ze względu na q, równanie różniczkowe drgań harmonicznych swobod-

nych o częstości kołowej a>o = 1 IjLC i okresie drgań T = 2jr/too ⁼ 2njLC.

■ Prąd / płynący w obwodzie otrzymujemy ze związku

/= ^ = -qa<o sin (a> / + 5) = q₀a) cos(co t + 5 +*).

Jak widać faza prądu wyprzedza fazę ładunku na kondensatorze o x/2. Napięcie na kondensatorze, które jest równe U_c =q/C, ma taką samą fazę jak faza ładunku na kondensatorze.

■ Energia obwodu drgającego LC jest zachowana ze względu na brak w nim oporu omowego, w którym wydzielałoby się ciepło Joule'a-Lenza powodując straty energii. Matematycznie oznacza to, że dE/dt musi być równe zeru. Prowadzi to do równania różniczkowego

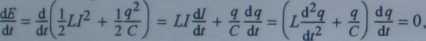
które po obustronnym podzieleniu przez dq/dt a następnie przez L daje, otrzymane wcześniej z II prawa Kirchhoffa, równanie różniczkowe drgań swobodnych.

■ Analogia drgań w obwodzie LC do prostego ruchu harmonicznego masy zawieszonej na sprężynie. Równanie drgań w obwodzie LC ma taką samą postać jak, w mechanice klasycznej, równanie drgań harmonicznych ciała o masie m, na które działa siła harmoniczna F=- kx mające postać

^+!*=o.

dt²

W analogii tej odpowiednikiem wychylenia x drgającego ciała z położenia równowagi jest ładunek na kondensatorze q, masie ciała wykonującego drgania mechaniczne odpowiada w elektrycznym obwodzie drgającym indukcyjność L, a odpowiednikiem współczynnika sprężystości k jest MC. Dodatkowo prąd I=dq /dt płynący w obwodzie jest odpowiednikiem prędkości v = dx/dt drgającego ciała.

Drgania elektromagnetyczne |    5

55. Drgania harmoniczne w obwodzie LC

ładunek na kondensatorze w pewnej chwili t

prąd płynący w obwodzie w pewnej chwili t

amplituda zmian ładunku

nakond	n /,'
W)=< '/(0=/o<	FqCOS(CO/ + 8) :os((D/ + 8 + ?) I -^---^ 1

faza początkowa drgań ładunku

amplituda natężenia prądu w obwodzie Iq = ggo

66.1 Okres drgań w obwodzie

częstość (kołowa) drgań co = -p=r

Jlć

okres drgań

T=2njLC

66.2 Energia obwodu drgającego LC

energia pola magnetycznego w cewce

energia obwodu drgającego LC

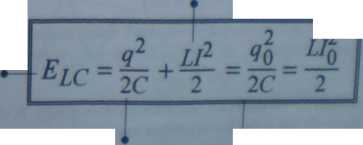
energia pola elektrycznego w kondensatorze

* maksymalna energia pola elektrycznego w kondensatorze

maksymalna energia pola magnetycznego w cewce

f