skanuj0005 (78)

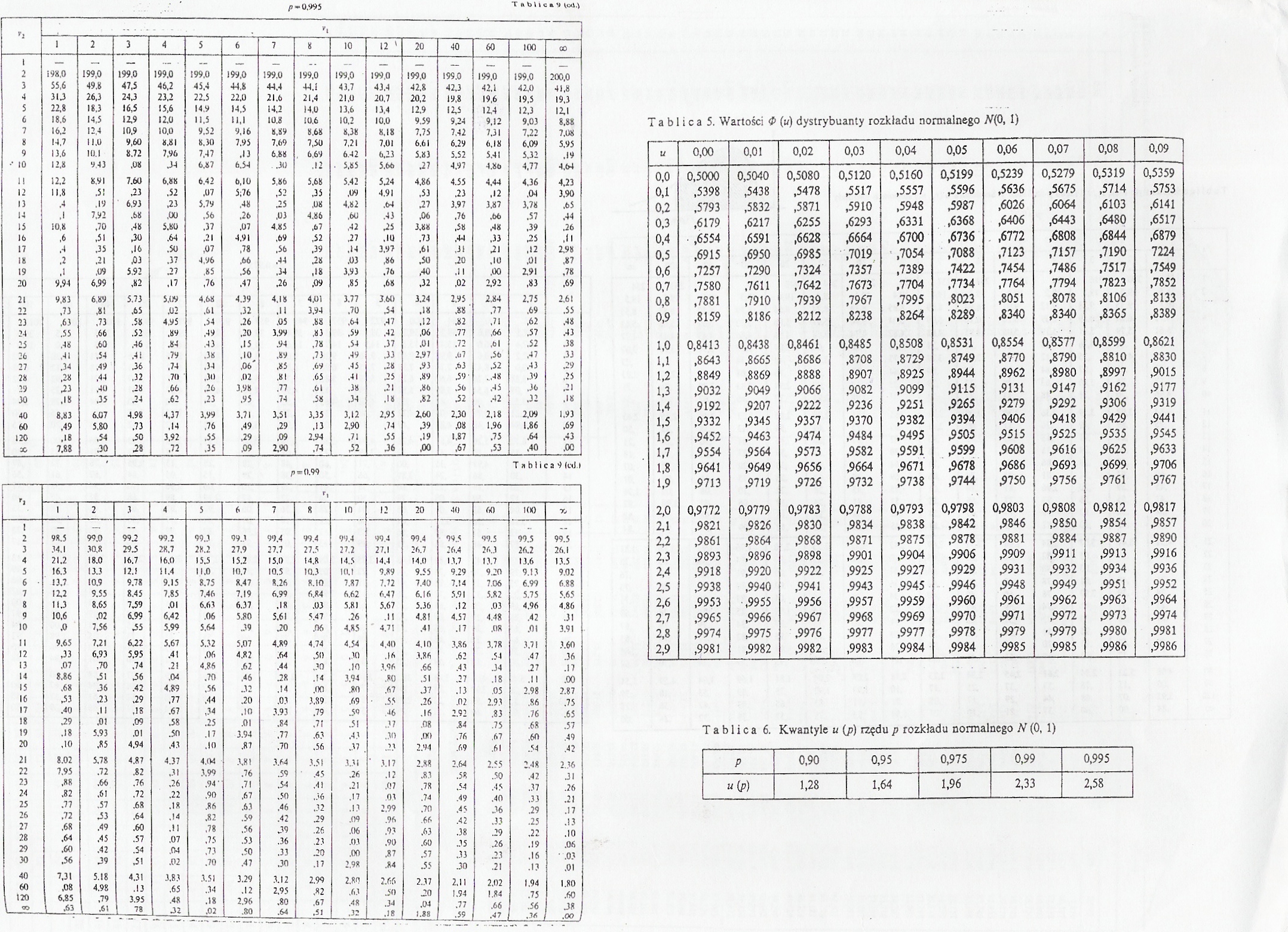
/!«• 0.995 T » *> l i c » >)

					.
	1	2	3	4	5	6	7	8	10	12 '	20	40	60	100	00
1 2	i 98,0	199,0	199,0	199.0	199.0	199,0	199,0	199,0	199,0	199.0	199,0	199.0	199,0	199.0	200,0
3	55,6	49.8	47,5	46,2	45,4	44,8	44,4	44.1	43.7	43.4	42.8	42,3	42.1	42,0	41,8
4	31J	26,3	24.3	234	22.5	22.0	21.6	21,4	21.0	20.7	20,2	19,8	19,6	19,5	19.3
5	22,8	18.3	16,5	15,6	14.9	14.5	14.2	14.0	13.6	13.4	12.9	12,5	12,4	12.3	12.1
6	18.6	14,5	12,9	12.0	II.S	U.l	10.8	10.6	10.2	10.0	9.59	9.24	9.12	9.03	8.88
7	16.2	12.4	10,9	10.0	9.52	9,16	8.89	8.68	8.38	8.18	7.75	7.42	7.31	122	7,08
8	14,7	11.0	9,60	8.81	8,30	7.95	7.69	7,50	7.21	7.01	6.61	6.29	6.18	6.09	5.95
9	13.6	1(1.1	8.72	7,96	7.47	.13	6.88	6,69	6.42	6.23	5.83	5.52	5.41	5.32	.19
•• 10	12.8	9.43	.08	.34	6.87	6.54	.30	.12	. 5,85	5.66	.27	4.97	4.86	4.77	4,64
11	12.2	8.91	7.60	6.88	6.42	6,10	5,86	5.68	5.42	5.24	4,86	4.55	4,44	4.36	4.23
12	11.8	,5!	,23	.52	.07	5;76	,52	,35	,09	4.91	.53	.23	.12	.04	3,90
13	,4	.19	6,93	.23	5.79	.48	45	.08	4,82	.64	21	3.97	3.87	3.78	.65
U	.1	7.92	.68	.00	.56	.26	.03	4.86	.60	.43	.06	.76	.66	.57	.44
li	10.8	,70	,48	5.80	.37	.07	4.85	.67	,42	.25	3,88	,58	.48	.39	.26
Ib	,6	,51	,30	.64	,21	4.91	.69	.52	.27	.10	.73	.44	.33	.25	.11
17	,4	.35	,16	.50	,07	,78	.56	.39	.14	3.97	.61	,31	.21	.12	2,98
18	.2	.21	.03	.37	4.96	.66	.44	.28	.03	,86	,50	.20	,10	.01	,87
19	,1	,09	5,92	47	.85	.56	.34	,18	3.93	.76	,40	.11	.00	2,91	,78
20	9,94	6.99	,82	.17	,76	.47	.26	,09	.85	.68	.32	.02	2 92	.83	.69
21	9,83	6.89	5.73	5.09	4.68	4.39	4.18	4.01	3.77	3.60	3.24	2.95	2.84	2.75	2,61
22	,73	.81	.65	.02	.61	.32	.11	3.94	.70	.54	.18	.88	.77	.69	.55
23	,63	.73	.58	4.95	.54	46	.05	.88	.64	.47	.12	.82	,71	,62	.48
24	.55	.66	.52	.89	.49	40	3.99	.83	.59	.42	.06	.77	,66	,57	.43
23	.48	.60	.46	.84	.43	.15	.94	,78	.54	.37	.01	.72	.61	.52	.38
26	.41	.54	.41	.79	.38	.10	.89	.73	.49	.33	2.97	.67	.56	.47	.33
27	.34	.49	.36	.74	.34	.06	.85	.69	.45	.28	.93	.63	.52	.43	.29
28	.28	.44	.32	.7(1	.30	,02	.81	.65	.41	.25	,89	.59-	..48	.39	,25
29	,23	,40	.28	.66	.26	3,98	.77	.61	.38	.21	.86	.56	.45	.36	.21
30	.18	.35	44	.62	43	.95	.74	.58	.34	.18	.82	.52	.42	.32	.18
40	8.83	6.07	4.98	4,37	3,99	3.71	3.51	3,35	3.12	2.95	2,60	2.30	2.18	2,09	1.93
60	.49	5.80	.73	.14	.76	.49	.29	.13	2.90	.74	,39	.08	1.96	1.86	.69
120	.18	.54	40	3.92	.55	.29	,09	2.94	.71	.55	.19	1.87	.75	.64	.43
X	7.88	.30	48	.72	,35	.09	2,90	,74	,52	J6	,00	.67	.53	.40	.00

	P,
	1	2	3	4	5	6	7	8	10	12	20	40	60	100	rj
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 40 60 120 i	98.5 34.1 21.2 16.3 13.7 12,2 11.3 10.6 .0 9.65 ,33 .07 8.86 .68 .53 .40 29 .18 ,10 8.02 7,95 ,88 .82 .77 .72 .68 .64 .60 .56 7.31 ,08 6,85 .63	99.0 30.8 18.0 13.3 10.9 9.55 8,65 .02 7.56 7.21 6.93 ,70 .51 .36 .23 .11 .01 5.93 .85 5.78 .72 .66 .61 .57 .53 .49 .45 .42 29 5.18 4.98 .19 .61	992 292 16.7 12.1 9.78 8.45 7,59 6.99 25 6.22 5.95 .74 26 .42 .29 ,18 .09 .01 4.94 4.87 .82 .76 .72 .68 .64 .60 .57 .54 .51 4.31 .13 3.95 78	99.2 28.7 16.0 11.4 9.15 7.85 .01 6.42 5,99 5.67 .41 .21 .04 4.89 .77 .67 .58 .50 .43 4.37 ,31 .26 .22 .18 .14 .11 .07 .04 .02 3.83 .65 .48 •33	99.3 28.2 15.5 11.0 8.75 7.46 6.63 .06 5.64 5.32 .06 4.86 .70 ,56 .-14 ,34 .25 .17 .10 4.04 3.99 .94' .90 .86 .82 .78 .75 .73 .70 3.51 .34 .18 .02	99.3 27.9 15.2 10.7 8.47 7.19 6.37 5.80 .39 5.07 4.82 .62 .46 .32 .20 .10 .01 3.94 .87 3.81 .76 .7! ,67 .63 .59 .56 .53 .50 .47 3.29 .12 2.96 .80	99.4 27.7 15.0 10.5 8.26 6.99 .18 5.61 .20 4.89 .64 ,44 .28 .14 .03 3.93 .84 .77 .70 3.64 .59 .54 .50 .46 .42 -39 .36 .33 .30 3.12 2.95 ,80 .64	99.4 27.5 14.8 10.3 8.10 6.84 .03 5.47 .06 4,74 .511 .30 .14 .00 3.89 .79 .71 .63 .56 3.51 .45 .41 .36 .32 .29 .26 .23 .20 .17 2.99 ,82 .67 .51	99.4 27.2 14.5 KU 7.87 6.62 5.81 .26 4,85 4.54 ,30 .10 3.94 .80 .69 .59 .51 .43 .37 3.31 .26 .21 .17 .13 .09 .06 .03 .00 2.98 2.80 .63 .48 .32	99.4 27.1 14.4 9.89 7.72 6.47 5.67 .11 4.71 4,40 .16 3.96 .80 .67 .55 .46 .37 .30 .23 ‘ 3.17 .12 ,07 .03 2.99 .96 .93 .90 .87 .84 2.66 .50 .34 .18	99.4 26.7 14.0 9.55 7.40 6.16 5.36 4.8! .41 4,10 3.86 .66 .51 .37 .26 .16 .08 .(KI 2.94 2.88 .83 .78 .74 .70 .66 .63 .60 .57 .55 2.37 .20 .04 1.88	99.5 26.4 13.7 9.29 7.14 5.91 .12 4.57 .17 3.86 .62 .43 .27 .13 .02 2.92 .84 .76 .69 2.64 .58 .54 .49 .45 .42 .38 .35 .33 .30 2.11 1.94 .77 .59	‘W. 5 26.3 13.7 9.20 7.06 5.82 .03 4.48 .08 3.78 .54 .34 .18 .05 2.93 .83 .75 .67 .61 2.55 .50 .45 .40 .36 .33 .29 .26 .23 .21 2.02 1.84 .66 .47	99.5 26.2 13.6 9.13 6.99 5.75 4.96 .42 .01 3.71 .47 .27 .11 2.98 .86 .76 .68 .60 .54 2.48 .42 .37 .33 .29 .25 .22 .19 .16 .1? 1.94 .75 .56	99.5 26.1 13.5 9.02 6.88 5.6J 4.86 .31 3.91 3.60 .36 .17 .00 2.87 .75 .65 .57 .49 .42 2.36 Jl .26 .21 .17 .13 .10 .06 .03 .01 1.80 .60 J8
				—	.......—	-------	-----	. ---					T---------'

Tablica 5. Wartości <P (») dystrybuanty rozkładu normalnego N{0, 1)

U	0,00	0,01	0,02	0,03	0,04	0,05	0,06	0,07	0,08	0,09
0,0	0,5000	0,5040	0,5080	0,5120	0,5160	0,5199	0,5239	0,5279	0,5319	0,5359
0,1	,5398	,5438	,5478	,5517	,5557	,5596	,5636	,5675	,5714	,5753
0,2	,5793	,5832	,5871	,5910	,5948	,5987	,6026	,6064	,6103	,6141
0,3	,6179	,6217	,6255	,6293	,6331	,6368	,6406	,6443	,6480	,6517
0,4	• ,6554	,6591	,6628	,6664	,6700	,6736	,6772	,6808	,6844	,6879
0,5	,6915	,6950	,6985	,7019	,7054	,7088	,7123	,7157	,7190	7224
0,6	,7257	,7290	,7324	,7357	,7389	,7422	,7454	,7486	,7517	,7549
0,7	,7580	,7611	,7642	,7673	,7704	,7734	,7764	,7794	,7823	,7852
0,8	,7881	,7910	,7939	,7967	,7995	,8023	,8051	,8078	,8106	,8133
0,9	,8159	,8186	,8212	,8238	,8264	,8289	,8340	,8340	,8365	,8389
1,0	0,8413	0,8438	0,8461	0,8485	0,8508	0,8531	0,8554	0,8577	0,8599	0,8621
1,1	,8643	,8665	,8686	,8708	,8729	,8749	,8770	,8790	,8810	,8830
1,2	,8849	,8869	,8888	,8907	,8925	,8944	,8962	,8980	,8997	,9015
1,3	,9032	,9049	,9066	,9082	,9099	,9115	,9131	,9147	,9162	,9177
1,4	,9192	,9207	,9222	,9236	,9251	,9265	,9279	,9292	,9306	,9319
1,5	,9332	,9345	,9357	,9370	,9382	,9394	,9406	,9418	,9429	,9441
1,6	,9452	,9463	,9474	,9484	,9495	,9505	,9515	,9525	,9535	,9545
1,7	,9554	,9564	,9573	,9582	,9591	,9599	,9608	,9616	,9625	,9633
1,8	,9641	,9649	,9656	,9664	,9671	,9678	,9686	,9693	,9699	,9706
1,9	,9713	,9719	,9726	,9732	,9738	,9744	2150	,9756	,9761	,9767
2,0	0,9772	0,9779	0,9783	0,9788	0,9793	0,9798	0,9803	0,9808	0,9812	0,9817
2,1	,9821	,9826	,9830	,9834	,9838	,9842	,9846	,9850	,9854	,9857
12	,9861	,9864	,9868	,9871	,9875	,9878	,9881	,9884	,9887	,9890
2,3	,9893	,9896	,9898	,9901	,9904	,9906	,9909	,9911	,9913	,9916
2,4	,9918	,9920	,9922	,9925	,9927	,9929	2931	,9932	,9934	,9936
2,5	,9938	,9940	,9941	,9943	,9945	,9946	294 8	,9949	,9951	,9952
2,6	,9953	,9955	,9956	,9957	,9959	,9960	,9961	,9962	,9963	,9964
2,7	,9965	,9966	,9967	,9968	,9969	,9970	291 \	,9972	2913	,9974
2,8	,9974	,9975	,9976	,9977	,9977	,9978	2919	-,9979	,9980	,9981
2,9	,9981	,9982	,9982	,9983	,9984	,9984	,9985	,9985	2986	,9986

Tablica 6. Kwantyle u (jp) rzędu p rozkładu normalnego N (0, 1)

P	0,90	0,95	0,975	0,99	0,995
u{p)	1,28	1,64	1,96	2,33	2,58