skanuj0011

20

przyrządu, ale w przypadkach, kiedy odstępy pomiędzy kolejnymi kreskami podziałki są duże, można przyjąć, że ta niepewność jest równa połowie działki.

Dla mierników cyfrowych przyjmujemy, że ostatnia wyświetlana cyfra jest niepewna.

2. A_k x- niepewności wzorcowania fabrycznego przyrządu; dla miemi-

kZ

ków wskazówkowych jest równa A_kx- y^-, gdzie k - klasa przyrządu, Z - jego zakres. Klasa miernika cyfrowego jest podana przez producenta w instrukcji obsługi łącznie ze sposobem obliczenia na jej podstawie dokładności pomiaru. (Więcej informacji o klasie miernika znajduje się w rozdziale 8.)

Na niepewność systematyczną obserwatora składają się:

1.    A₀x - szerokość wskazówki miernika wyrażona w jednostkach skali,

2.    A_e x - szerokość obszaru drgań wskazówki (lub wyświetlacza w miernikach cyfrowych), wyrażona w jednostkach skali.

Tak, więc maksymalna niepewność systematyczna jest równa:

Ax_s = A^ + A^-t-A₀x + A_cx .

W przypadku, gdy niepewności A_kx, A₀x, A_ex są małe w porównaniu z A_dx możemy przyjąć, że niepewność systematyczna jest równa najmniejszej działce. Jeżeli jednak odstępy pomiędzy kolejnymi kreskami podziałki są dostatecznie duże i wyraźne, to możemy oszacować, że niepewność ta jest równa połowie, a czasem nawet 1/4 najmniejszej działki.

4.4. Całkowita niepewność pomiaru

Na całkowitą niepewność pomiaru składają się: niepewność systematyczna i niepewność przypadkowa. W praktyce laboratoryjnej często zdarza się tak, że jedna z nich jest znacznie większa od drugiej. Jeżeli różnią się co najmniej o jeden rząd wielkości, to możemy tę mniejszą zaniedbać w porównaniu z drugą większą. Wynika stąd, że w przypadku, gdy niepewność systematyczna jest znacznie większa od przypadkowej, nie ma potrzeby wykonywać serii np. dziesięciu pomiarów. Nasuwa się zatem pytanie, w jaki sposób bez obliczania niepewności przypadkowej S_x określić optymalną liczbę pomiarów¹. Najczęściej postępujemy w następujący sposób: wykonujemy próbną serię pomiarów i badamy relację między niepewnością systematyczną Ax (patrz rozdział 4.3) a rozrzutem, czyli różnicą między wynikiem maksymalnym i minimalnym (*ma* - *min)- Możliwe są trzy sytuacje:

1)    Ax«x„„ - x,,

J    max    min^J

2)    Ax » x _v - x. ,

J    max    min >

3)    Ax ~ x_m„ - x_m- .

'    max    min

Przyjmujemy, że nierówności są spełnione, gdy obie strony różnią się co najmniej o jeden rząd wielkości.

W punkcie pierwszym niepewność przypadkowa jest znacznie większa od systematycznej. Możemy więc zaniedbać niepewność systematyczną i przyjąć, że niepewność pomiarowa jest równa niepewności przypadkowej. W sytuacji drugiej dominuje niepewność systematyczna, a więc za niepewność pomiarową przyjmiemy niepewność systematyczną. Przypadek trzeci odpowiada sytuacji, gdy obydwie niepewności są porównywalne. Wtedy maksymalna niepewność średniej arytmetycznej Ax_miX jest równa sumie niepewności systematycznej oraz maksymalnej niepewności przypadkowej:

'^^cmax ~    ⁺ 3S_X .

Przy liczbie pomiarów n < 10 zamiast czynnika 3 należy wziąć odpowiedni współczynnik Studenta-Fischera odpowiadający poziomowi ufności a- 0,99.

W praktyce czasem stosuje się również wzór na całkowite odchylenie standardowe średniej arytmetycznej:

a

c

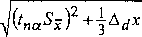
2

W laboratorium studenckim liczbę pomiarów uzgadniamy z osobą prowadzącą ćwiczenie.