skanuj0012

22

5. Niepewności pomiarów pośrednich

5.1. Obliczanie niepewności przypadkowych pomiarów pośrednich

Większość wielkości fizycznych nie da się zmierzyć bezpośrednio przyrządami. Chcąc je wyznaczyć musimy skorzystać z praw fizycznych, które pozwalają je wyrazić poprzez zależności funkcyjne, w których występują inne wielkości, mierzone bezpośrednio.

Załóżmy, że wielkość fizyczna y jest funkcją wielkości x_]t jc₂,......*»,. nieza

leżnych w sensie rachunku prawdopodobieństwa:

y = f{x„x₁,......x„).    (15)

W celu doświadczalnego wyznaczenia wartości wielkości y wykonujemy serie pomiarów wielkości xi,x₂........x„, obliczamy średnie x\,X2,.......x„ oraz odchylenia standardowe    ,......Sj . Wielkość najbardziej prawdopodobna

y jest równa:

y-f{xi,*2> *»)■

Natomiast średnia niepewność kwadratowa 8y (odchylenie standardowe pomiaru pośredniego lub inaczej błąd średni kwadratowy) wielkością jest równa:

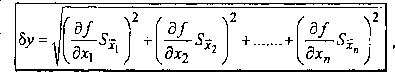
(16)

gdzie to pochodna cząstkowa funkcji (15) w punkcie x = (jcj, X2,....x„). dx,

5.2. Obliczanie niepewności maksymalnych

Nie zawsze w trakcie pomiaru pośredniego możemy każdą wielkość x,- wyznaczyć wielokrotnie. Najczęściej wykonujemy po jednym pomiarze każdej wielkości x_t, więc nie jesteśmy w stanie wyliczyć odchylenia standardowego (16). W takim przypadku obliczamy niepewność maksymalną. Stosujemy wte-

dy metodę różniczki zupełnej. Niech Ax\, Ax₂,......Ax„ oznaczają odpowiedn

niepewności maksymalne wielkości jcj, x₂,......jc„ (patrz 4.4). Różniczka zup-

na funkcji (15) jest równa:

dy:

df , df

dx, + dx, +.

3x.

dx_n

5x„    "

Zastępując we wzorze (17) różniczki dr,- przez przyrosty skończone (niepr.-no-ści maksymalne) Ax_t oraz uwzględniając, że maksymalną niepewno

wielkości y‘ otrzymamy wtedy, gdy wszystkie przyczynki    będą min

dx;

ten sam znak, otrzymamy wyrażenie na niepewność maksymalną Ą>w (W maksymalny):

A v =		+		*f.......+	df A -Ar„
	dx{ ^1		dx2		dxn

Miarą dokładności metody pomiaru jest niepewność względna <r_w {zwm również błędem względnym) zdefiniowana jako stosunek niepewności pi miarowej Ay _max (lub 8y danej wzorem (16)) do wyniku pomiaru y:

a

W

(lub

_

y

)■

W szczególnym przypadku, gdy wielkość fizyczna y mierzona pośredni jest iloczynem potęg wielkości prostych xi, x₂,......x„:

y = Ax i^¹ • x-i¹ •.....• x^ⁿ , A- dowolna stała,

bardzo łatwo można obliczyć maksymalną niepewność względną (maksymalny błąd względny):

N -	Kj <3 | -i*r	+	$	+........4*	, Ax, k„-
^ y	*1		^xi