skanuj0085

I /I)

0_E = JJE{P) o dS = JJ/?(P) o n{P) ÓS,    (3)

s    s

gdzie dS to nieskończenie mały element powierzchni S, n(P) - jednostkowy

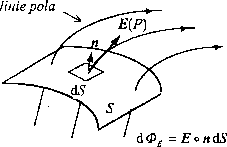
Rys.2. Strumień pola przechodzącego przez powierzchnię S

wektor normalny do powierzchni S w punkcie P, wyróżniający jedną ze stron S (mówimy wtedy o zorientowanej powierzchni S), a znak: „ ° ” oznacza iloczyn skalamy dwu wektorów:

dS(P) = n(P) ■ dS

Strumień pola 0_E jest wielkością skalarną. Gdy pole E jest jednorodne, a S jest płaską powierzchnią o wielkości S, wtedy n nie zależy od punktu na S i jeżeli zdefiniujemy wektor: S = n -S, gdzie S = |iS|, to strumień pola w tym przypadku dany jest wzorem:

<J>_£ = E°S - EScosa,    (5)

gilzie E=\E\ i S= |5j.

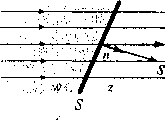
Strumień pola jest więc dodatni, gdy linie przechodzą z „wnętrza” powierzchni (oznaczonego jako w na rys.3) na jej stronę ~    „zewnętrzną” (z na rys.3), tj. tą którą

£    orientujemy w przestrzeni polem wek-

-    torów n (a ogólniej n(P), gdzie PzS), a

-    ujemny - gdy jest odwrotnie. Należy pamiętać, że orientacja powierzchni S, tzn. to, która strona powierzchni jest zew-

Rys.3. Orientacja płaszczyzny S    nętrzna, a która jest wnętrzem, jest umo

wą.

Natężenie pola E, linie natężenia pola i strumień pola, są w teorii pola elek-I tycznego pojęciami związanymi z tzw. wektorowym obrazem pola.

1.4. Potencjał elektryczny ę

Siły pola elektrycznego są siłami zachowawczymi, zatem praca L_PB wykonana przez te siły przy przesuwaniu ładunku próbnego qo pomiędzy dwoma punktami pola P i B nie zależy od drogi i równa jest ujemnej zmianie energii potencjalnej E_P, a stąd:

B    B

AE_p=E_p(B)-E_p{P) = -L_PB=-]F°dr = -q₀\Eodr.

p    p

Różnicą potencjałów między punktami P i B nazywamy iloraz zmiany energii potencjalnej i ładunku:

AE    ^B

(p{B) - ę{P) = —- = - f E o dr.

9o    p

Często przyjmuje się, że w pewnym umownym punkcie pola B (np. w nieskończoności lub na powierzchni Ziemi) potencjał ma wartość 0. Wówczas:

<p(P) = —-    (6)

?o

Zatem fizycznie potencjał (fjP) pola elektrycznego w pewnym jego punkcie P jest ilorazem pracy L_PB wykonanej przez siły pola przy przemieszczaniu ładunku próbnego qo z punktu P do punktu B w nieskończoności, i ładunku przenoszonego q₀ (rys.4).

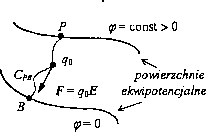
Rys.4. Przesunięcie ładunku próbnego z punktu P do B przez siły pola

Powierzchnią ekwipotencjalną nazywamy miejsce geometryczne punktów o stałej wartości potencjału.

Jednostką potencjału, określaną ze wzoru (6) jest w układzie jednostek SI IV. Jest on zarazem jednostką napięcia, czyli różnicy potencjałów w tym układzie.

Praca L_PB po dowolnej drodze C_PB nie zależy od kształtu drogi łączącej P i B. Zatem i ę nie będzie od niej zależał. Jest to ogólna własność pól potencjalnych.