Strona0045

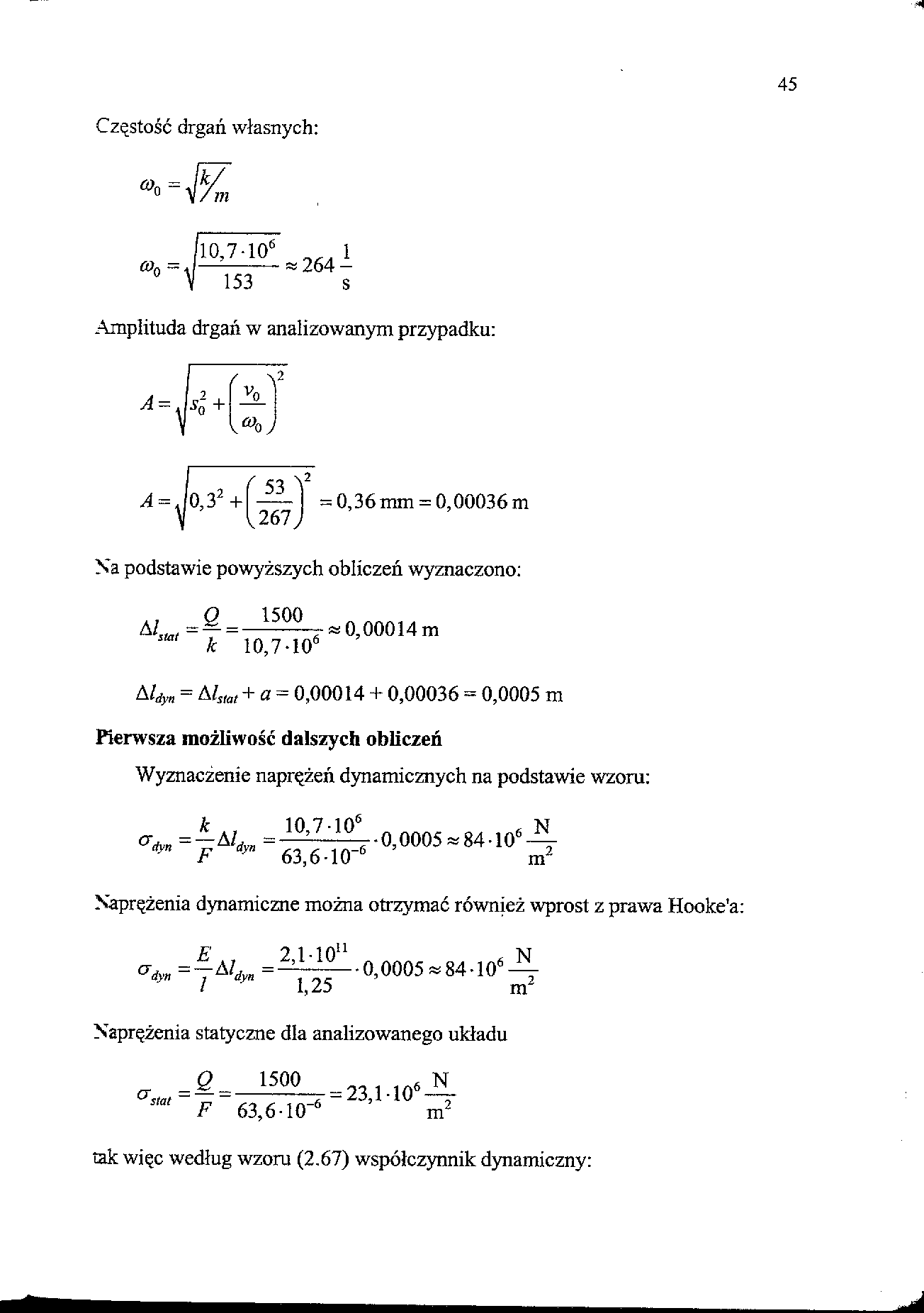
Częstość drgań własnych:

-i

^^ll° ~ 264 -

153    s

Amplituda drgań w analizowanym przypadku:

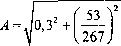
= 0,36 mm = 0,00036 m

Na podstawie powyższych obliczeń wyznaczono:

AL

Q _ 1500 k ~ 10,7*10⁶

0,00014 m

Aldyn = A l_stat+a = 0,00014 + 0,00036 - 0,0005 m Pierwsza możliwość dalszych obliczeń

Wyznaczenie naprężeń dynamicznych na podstawie wzoru:

0,0005 = 84-10⁶

k_ 10,7-10⁶ f⁴'"" 63.6-10^-6

Naprężenia dynamiczne można otrzymać również wprost z prawa Hooke'a

E _A1    2,MO¹¹

⁷dyn j &^ldyn ~~    ^5

*0,0005 ~84*10⁶^-

Naprężenia statyczne dla analizowanego układu

Q ^    1500

F ~ 63,6-10“^ó

- 23,1-10'

N

tak więc według wzoru (2.67) współczynnik dynamiczny: