Strona0164

sin <uf

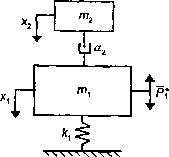
Rys. 7.9

Interesują nas tylko drgania wymuszone. Ich całki szczególne mają postać:

~ Ą _l sin cot + A_n cos cot x₂ =A_2] smmt + ^2 costó/

(7.35)

Aby wyznaczyć amplitudy drgań obu mas, zapiszemy wyrażenia (7.35) w następującej formie:

x₁=A_l sm{mt + ^) x₂ - A₂ sin(ótf + <p₂)

(7.36)

gdzie: Ą =    Ą = \j4i+4i-

Po podstawieniu całek (7.35), a także ich pierwszych i drugich pochodnych oraz przyrównaniu współczynników przy sin cot i costttf do zera otrzymano układ czterech równań algebraicznych, z których wyznaczono A_u, A_i2, A₂u A₂₂, a następnie amplitudy drgań A\iA₂ mas mi i m₂.

1

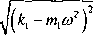
'l 0    9    4

a₂ar -m₂<o

m\m^A + a₂co²^m_] + m₂)co²

_a₂(t)_

ml&⁴ + a\(o² £(mj + m₂ ) co²

Pierwszą zależność (7,37) można przedstawić w postaci

(7.37)