Strona0178

178

przy n — 4

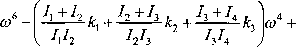
k_}k₂ +

I_x+I₂ I₃+I

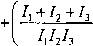
1^J2^J3^J4

hh hh

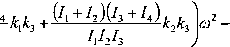
(8.7)

7] + J₂ ⁺h +1*

Przy dużej liczbie kół otrzymane równanie częstości drogą rozwijania wyznacznika wymaga długich obliczeń. Dlatego do obliczenia drgań skrętnych w tych przypadkach stosuje się inne sposoby. Po wyznaczeniu z równania częstości wartości częstości własnych drgań skrętnych układu i podstawieniu ich do równań (8.3) otrzymamy związki między amplitudami drgań kół w każdym z głównych drgań, które określają postacie drgań głównych (rys. 8.9). Za pomocą tych wykresów wyznacza się węzły, tj. przekroje wału, które pozostają nieruchome.

Drgania wymuszone wału mogą być wywołane działaniem zmiennych momentów obrotowych przyłożonych do odpowiednich kół. Drgania te powodują zmęczenie wału, wskutek czego może on ulec zniszczeniu. Równania różniczkowe drgań wymuszonych dowolnego układu kół różnią się od równań różniczkowych drgań skrętnych swobodnych występowaniem po prawej stronie równań momentów wymuszających przyłożonych do kół, np.

M_i=M_i0co&GJt

Rozwiązanie szczególne ma postać:

^-ć^COStóf

(8.8)

<p₂ = a₂ cos cot

ę_n —a_n cos ćot

gdzie: a_u ..., a„ - szukane amplitudy kątowe drgań kół.

Podstawiając (8.8) do równań drgań wymuszonych, otrzymujemy równania do wyznaczenia amplitud drgań wymuszonych a_u a₂,..., a„. Po otrzymaniu amplitudy można zbudować wykres przedstawiający postacie drgań wymuszonych wału (rys. 8.10). Z wykresu można znaleźć przekroje wału, które nie biorą udziału w drganiach. Wartość momentów skręcających M_sj dla odpowiednich odcinków wału wyznacza się wg wzorów: