0000040 2

<.x.y>c6° <=> [V (U_a .^(jc.y)] A [ V -^(y.X)]

Z określonla tej relacji wynika, że jeot ona zwrotna, oymetry-czna i przechodnio. Oeat zatem relacją równoważności, która dziali zbiór wierzchołków X na jej rozłączne klaoy obotrekcji 1 tym samym dziali graf (hlpergraf) na ekłodowa ollnoj epój -noócl.

Składowo allnaj spójności Jeat to maksymalny podgraf, który jeat grafea ailnie opójnyo.

Ilość składowych silnej spójności oznaczymy przez 3£^D(G)

1 4 JC*(G) 4 n; n • |X|

Efaktywnya algorytmom wyznaczania wszystkich składowych silnej spójności jest olgorytm Lelfmane [29] opisany w rozdzlolo 6. dotyczącym dróg w grafach skierowanych.

5.4. Łańcuchy najkrótoze

Oznoczymy przez ^ (x^p,x^k) łańcuch

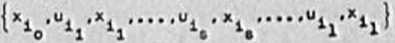
dla którego x. •

d k°    *

Przez t(*^p,x ) oznaczymy zbiór różnych łańcuchów

Długość każdego łońcucha jest równo 1 x^p ,x^k )J .

oroz

Ł a

ustalone

ń c u c h e

najkrótszy

dwa wierzchołki

^_Bi_n(^xP.* )€Ł(^xP.^x ). <*!« którego

nazywamy

{•£_ł(«^p.x^k)}.

łoczgcym

łańcuch

¹[y«inł^xP‘^xk>]- ^{Bin 1} [^₁(x^P.x^k)]

ijCŁOW

Hożo być wiele różnych łańcuchów najkrótszych w zbiorze *Ł(x^p,x^k).

TWIERDZENIE 5.8

Oeóli łańcuch jest najkrótezy, to jest łańcucha# prootyn.

Dowód tago twierdzenia nożna pooinęć za względu no oczywistość jago tezy.

TWIERDZENIE 5.9

Łańcuch jaot najkrótszy wtedy 1 tylko wtedy, gdy każdy jago odcinek jest odpowiednim łańcuchem najkrótszym.

O o w ó d s

Oeśli każdy odcinak jest łańcuchem najkrótszym, to oczy -wlóclo 1 cały łańcuch, jako azczególny odcinek, jest najkrótszy. Wystarczy zetem dowieóć, że Jeżeli łańcuch ^_mi_n(^xP.*^k) Jeat najkrótszym, to każdy odcinek tego łańcucha jest odpowiednia łańcuchem najkrótszym. Załóżmy przeolwnle, że istnieje odcinek

Sytuaojs taka jest możliwa tylko w tym przypadku, gdy niektóre gałęzie tworzęce łońcuch m^^xi'^xi) występuję w łańcuchu i_rln(x^p,x^k) przed wierzchołkiem lub po wierzchołku Xj. Wtedy Jednak można skrócić łańcuch ^min(^xP*^xk)* ^{00 #toi w} sprzeczności z definicję łańcucha najkrótszego 1 przeczy założeniu. Uzyskana sprzeczność kończy dowód twierdzenia.

Teza twierdzenia 5.9 umożliwia zastosowanie motody programowania dynamicznego (patrz 0.2) do wyznaczanie łańcuchów najkrótszych, łęczęcych ustalony wierzchołek x^p z pozostałymi wlerzchołkooi grafu (hipergrefu), epójnyoi z wierzchołkiem x^p. Etapy toj metody okreólajo następująco podzbiory wierzchołków]

^x0*..	. j ,	gdzie
^xo •	{*1 .
^X1 •	(*, ^£ * \ *0 ■	r13 > 0 A «1 e x„}
•	k*f	^%
^xk •	{*3 ^tX\yo^x.	i ^rij > o a e

79