0000099

puetowoóć alnloolncgo przekroju rozdzielajęcego..Zotea w prek-tyce pojęcie co aa dule znaczenie zarówno przy projektowaniu ■leci transportowych, Jok 1 przy planowaniu przewozów w letnie-JęceJ alecl. W przypadku dużych sieci, zadanie zoplanowanla przepływu maksymalnego nie Jest proste. To samo nożna powie -dzleć o wyznaczaniu alnimalnego przekroju rozdzlelojęcogo. Zatoń, metodo wyznaczania maksymalnego przepływu na duże Znaczenie dla zastosowań praktycznych. Metodę tekę nożna uzyekać będż przez sfornułowanlo problemu jako zadania progronowanle linio -wogo, będż przez wykorzystanie konstrukcji przekroju rozdzielającego, zawartej w dowodzie twierdzenia 11.1. Ten drugi eposób prowadzi do algorytau bardziej efektywnego 1 z tego względu,dla zrozumienia istoty algorytmu, warto zapoznać się z dowodom tego twierdzenia, tym bordziej że wynlksjęcy z niego algorytm wyznaczenie naksynelnego przepływu stanowi letotnę częóć większości algorytmów wyznaczania przepływów 1 opływów optynalnych w sieciach skierowanych.

TWIERDZENIE 11.1 (Ford-Fulkerson)

Wartość maksymalnego przepływu v(f^ą) jest równa przepustowości minimalnego przekroju rozdzielajęcego H(P*).

Dowód i

W celu uproszczenia zapisu przyjnujeay, że każdy przekrój rozdzlelajęcy P Jest równoważny odpowiedniej parze podzbiorów wierzchołków (X₁,X₂) i wprowadzimy naetępujęce oznaczenia

C f(*.y) • F(*'X) ytfyo

y??^V^V'^X) " ^F*^X'^X)

z:f(*,y) - f(x,.x₂)

2Zh(x.y) - M(X-.X₂)

<vg>eP    ^ł

L a a.a t

De żali (X₁,X₂) jest przekrojea rozdzielaJęcya sieci, a f przepływaa w taj sieci, to

v(f) - F(X_x.X2) - F(X₂,X₁)^H(X₁.X₂)

Dowód 1 o a o t u. Ole dowodu równości wystarczy zapisać

V'

(f) - C [f(x.X) - F(X.x)] x€X^

Rówooóć ta jeet prawdziwo, ponieważ tylko dla x ■ a składnik pod cumę jeot niezerowy 1 równy v(f), natomiast a 4 Xj. Rozpl-• ujęc prowę stronę równości, otrzymujemy

E[f(x,X) - F(x.x)] . F(X_ł,X) - F(X.X₁) -

i

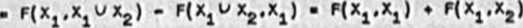
- F(X₁,X_ł) - F(X_z,X_ł) . F(X₁.X₂ł - F(X₂.X₁)

Ola dowladzanla nierówności v(f) i H<X_1#X₂) zauważmy, żt F(X₁,X₂)<H(X₁,X₂), natomiast F(X₂,X₁)>0. Kohczy to dowód la -matu.

Dowód twiardzanla i Z taty lamatu otrzymujemy w szczególności

v(f’X H(xJ. xj)

I *    ), to p będzie przekrojem minimalnym i teza twier

dzenia będzie dowiedziona, ponieważ każdy inny przekrój mini -molny P* będzie nleł tę sarnę, einlmalnę przapuetowość H(P^F).

Konotrukcja przakroju P^F .(zbioru xj)i Ola założonego przepływu maksymalnego f*, realizujemy naatępujęcę procedurę i

o

i Do X_Ł zaliczamy źródło a. Zbiór X_x nazywamy zbiorem ocechowanych i niesprawdzonych wierzchołków.

197