040

Równania i nierówności wielomianowe

Odpowiedź

x e {-2, -6, 2, 6}

ZADANIE 3

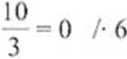
Równanie uporządkuję, pozbywając się ułamków.

P--

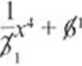
2x* + .v² - 20 = 0 Niech a*² = t 21² + 1-20 = 0

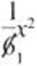
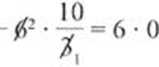
Otrzymuję równanie kwadratowe, gdzie a = 2. Z) = 1. c = -20.

Liczę A =    - 4aci pierwiastki.

t

A =I²-4 • 2 • (-20) = 1 + 160= 161

VA = VT6l

-i - nTóT -(i + vi6T)

'■⁼    4    4

-1 + \i61 V16 f - 1

4    4

I teraz pułapka!

Jeden z pierwiastków jest ujemny, bo \I 61 * 12,68857. Należy wrócić do podstawienia.

(*) a² =

-(1 + n-TóT)

lub

(**) *² =

VI61 — 1

Równanie (*) nie ma rozwiązania w zbiorze liczb rzeczywistych, ponieważ liczba

-(i + VT6l) _:Q

4

Równanie (**) ma dwa rozwiązania ponieważ liczba

VI61 - 1

lub

czyli x e 0

YTói i

< )d powiedź

JnTóT -1

lub

,.JĘT

ZADANIE 4

To równanie jest dwusześcienne, bo = (X^{1 2}}*' (ze wzoru: (ar)' = ar "). Równanie sprowadzamy do kwadratowego przez podstawienie.

Teraz stosuję wzory na A i pierwiastki: A = b² - 4 jc.

79

1

x⁶ + 2x^}- 15 = 0 Niech x* = /

(.v³)² + 2.v³ - 15 = 0 z²+ 2/- 15 = 0

A = 2² - 4 • 1 •(-15)= 4 + 60 = 64

= \64 = 8

-2-8 -10 .

/, =—— = —= - 5 ¹ 2 2

-2 + 86 „

=₂-=³

Wracamy do podstawienia

2

tutaj już nie ma pułapki, bo pierwiastek trze-

X = /. Czyli A'³ — -5 lub A*³    3.    ciego stopnia z liczby ujemnej istnieje (w R).

Zatem x = -\5 lub x = >/3 Odpowiedź

.v = -\’5 lub .v = \'3

Jak pamiętasz, każdy wielomian o współczynnikach rzeczywistych można rozłożyć na czynniki liniowe lub czynniki stopnia drugiego nierozkładalne. Rozwiązując równanie wielomianowe, najpierw postaramy się rozłożyć na czynniki możliwie najniższego stopnia, czyli liniowe. Mamy kilka sposobów, za pomocą których możemy rozłożyć wielomian na czynniki.