045 7

prędkością, poją odpowiednie dkość v. z jak. emskim).

2.

= 29 <41 - 4,9t-

2    3    4    5    6 t'~

funkcji h opisując-. na jakiej znajd -kula w chwili t.

3.

Na Marsie przyspieszenie grawitacyjne wynosi około 3,7 m/s², zatem funkcję opisującą drogę przebytą przez swobodnie spadające ciało można przedstawić w postaci s(t) = 1,85£²,’ gdzie droga mierzona jest w metrach, a. czas w sekundach. Oblicz prędkości w chwili t = 4, jakie osiągnie swobodnie spadające ciało na Ziemi oraz na Marsie. Odpowiedź podaj w km/b.

-    29,4 - 9,81

2    3\ 4 $6 tV

\

' \

Ciało wyrzucone pionowo w górę z powierzchni Marsa z prędkością początkową vq = 18,5 m/s znajduje się w chwili t na wysokości:

h(t) = 18,51 - 1,85t²

Oblicz prędkość, z jaką poruszało się to ciało w chwili t — 5.

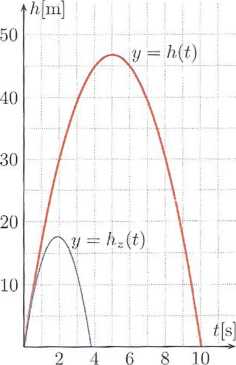
Na rysunku obok przedstawiono wykres funkcji: h(t) = 18M - l,85t² oraz dla porównania wykres funkcji: h_z{t) = 18,5t — 4,9t²

opisującej wysokość, na jakiej znajdowałoby się w chwili t ciało wyrzucone z tą samą prędkością początkową z powierzchni Ziemi.

v(t_Q) v(t)

Przypuśćmy, że punkt porusza się po osi liczbowej, —+-a funkcja v opisuje jego prędkość w zależności od czasu t.

\

\

.......I.............:.......^:\

\

i i \

- funkcji v opisujące. z jaką poruszała chwili t.

mianie zwrotu wekter

Przyspieszenie średnie w przedziale od to do t wyraża się za pomocą wzoru:

O,ar -

t-to

Przyspieszenie a(to) w chwili to jest pochodną prędkości:

,, ,    ,. v(t)-v(to)

a{to) = hm ——-

t—yto t Zq

bodnie ciało opisu; letrach, a czas w i to = 3. Odpowie :

4.    Prędkość, z jaką punkt porusza się po osi liczbowej, opisuje funkcja v. Oblicz przyspieszenia w chwilach t = 1 oraz t = 4.

a) v(t) = 41,    b) v(t) — t² — t    c) v(t) = £'³ — 4t² + t

5.    Wysokość w metrach, na jakiej znajduje się kula wystrzelona pionowo w górę, jest opisana za pomocą funkcji h(t) — 24,51 — 4,9t². Wyznacz funkcje opisujące prędkość i przyspieszenie tej kuli.

5.11. Interpretacja fizyczna pochodnej 297