078 079 2

78 Programowanie liniowe

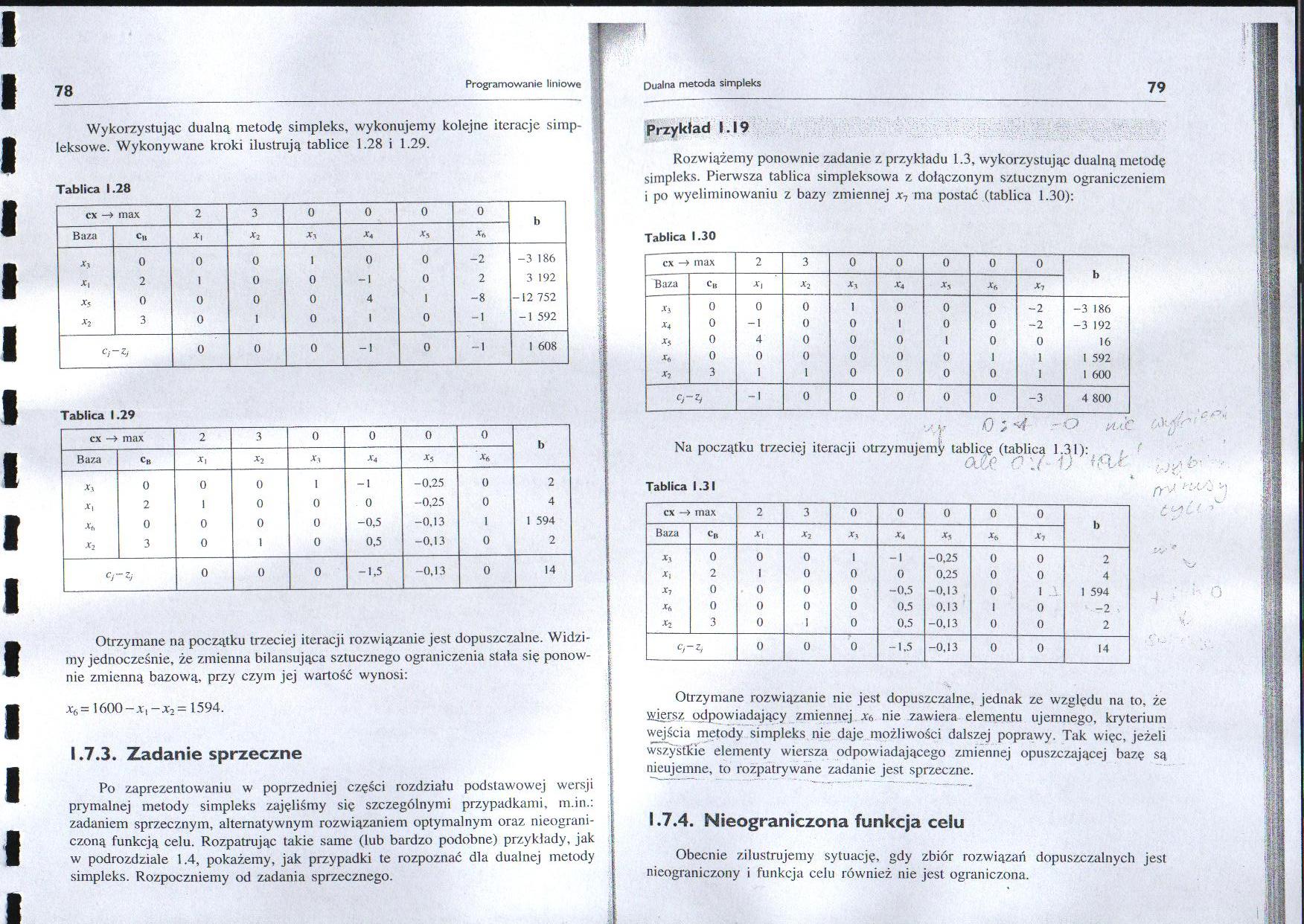
Wykorzystując dualną metodę simpleks, wykonujemy kolejne iteracje simpleksowe. Wykonywane kroki ilustrują tablice 1.28 i 1.29.

Tablica 1.28

cx —»	max	2	3	0	0	0	0	h
Baza			Xi	Xy	XĄ	Xs	Xh
X*	0	0	0	i	0	0	-2	-3 186
X,	2	1	0	0	-1	0	2	3 192
JC5	0	0	0	0	4	1	-8	-12 752
^x2	3	0	1	0	1	0	-1	-1 592
^et	-Z,	0	0	0	-1	0	-1	1 608

Tablica 1.29

cx —>	max	2	3	0	0	0	0	b
Baza	CB	*1	*2	Xy	Xą	x*	*6
x%	0	0	0	i	-i	-0.25	0	2
x,	2	1	0	0	0	-0,25	0	4
X(i	0	0	0	0	-0,5	-0,13	1	1 594
*2	3	0	1	0	0,5	-0,13	0	2
^cr	- 7 ■	0	0	0	-1,5	-0,13	0	14

Otrzymane na początku trzeciej iteracji rozwiązanie jest dopuszczalne. Widzimy jednocześnie, że zmienna bilansująca sztucznego ograniczenia stała się ponow- j nie zmienną bazową, przy czym jej wartość wynosi:

jc₆= 1600-je,-** =1594.

1.7.3. Zadanie sprzeczne

Po zaprezentowaniu w poprzedniej części rozdziału podstawowej wersji prymalnej metody simpleks zajęliśmy się szczególnymi przypadkami, m.in.: zadaniem sprzecznym, alternatywnym rozwiązaniem optymalnym oraz nieograniczoną funkcją celu. Rozpatrując takie same (lub bardzo podobne) przykłady, jak w podrozdziale 1.4, pokażemy, jak przypadki te rozpoznać dla dualnej metody simpleks. Rozpoczniemy od zadania sprzecznego.

Przykład 1.19

Rozwiążemy ponownie zadanie z przykładu 1.3, wykorzystując dualną metodę simpleks. Pierwsza tablica simpleksowa z dołączonym sztucznym ograniczeniem i po wyeliminowaniu z bazy zmiennej x₇ ma postać (tablica 1.30):

Tablica 1.30

cx ->	max	2	3	0	0	0	0	0	b
Baza	Cli	X,	^x2		Xą			•*7
Xi	0	0	0	1	0	0	0	-2	-3 186
*4	0	-1	0	0	1	0	0	-2	-3 192
*5	0	4	0	0	0	1	0	0	16
	0	0	0	0	0	0	1	1	1 592
*■>	3	1	1	0	0	0	0	I	1 600
Ci-	-*/	-1	0	0	0	0	0	-3	4 800

Na początku trzeciej iteracji otrzymujemy tablicę (tablica 1.31):

aie. o U V mr

rr^v

Tablica 1.31

cx -»	max	2	3	0	0	0	0	0
Baza	^CB	x,		X*	*4		x*	*7
Xi	0	0	0	i	-1	-0,25	0	0	2
^xt	2	1	0	0	0	0.25	0	0	4
*7	0	0	0	0	-0.5	-0,13	0	1 '.	1 594
Xf>	0	0	0	0	0,5	0,13	1	0	-2
x2	3	0	1	0	0,5	-0,13	0	0	2
c,-	-Zj	0	0	0	-1,5	-0,13	0	0	14

Otrzymane rozwiązanie nie jest dopuszczalne, jednak ze względu na to, że \viersz odpowiadający zmiennej Xb nie zawiera elementu ujemnego, kryterium wejścia metody simpleks nie daje możliwości dalszej poprawy. Tak więc, jeżeli wszystkie elementy wiersza odpowiadającego zmiennej opuszczającej bazę są nieujemne, to rozpatrywane zadanie jest sprzeczne.

1.7.4. Nieograniczona funkcja celu

Obecnie zilustrujemy sytuację, gdy zbiór rozwiązań dopuszczalnych jest nieograniczony i funkcja celu również nie jest ograniczona.