081(1)

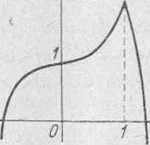
i x --- 1 jest ona wklęsła, a na prawo od punktu x — 1 znowu jest wypukła (rys. 68). Rzędne punktów przegięcia obliczamy z równania krzywej, podstawiając odpowiednie odcięte: y(0) = 1, y(l) = 2. Punkt przegięcia

y\ y = 2-\x^s-A

x

Rys. 68

(1, 2) pokrywa się z punktem krzywej, w której rzędna ma maksymalną wartość.

Znaleźć punkty przegięcia i przedziały wklęsłości i wypukłości krzywych:

378. y = x³-3x²-9xj-9 380. y = 1 — ln (jc² — 4) 382. y = arc tg

384*. y = arc sin —

379. y = x+36x²-2x³-x* 381. y = ję-ł-2— \'^rx-

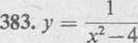
385*. y = 1- \ x²—2\

§ 8. Asymptoty

Asymptotą krzywej nazywamy prostą, do której zbliża się rdeograniczenie punkt krzywej oddalający się nieograniczenie od początku układu współrzędnych.

Krzywa może zbliżać się do swej asymptoty w taki sam sposób, jak zmienna zbliża się do swej granicy; może więc ona, tak jak w zad. 386 (1), pozostawać po jednej stronie asymptoty, bądź też może znajdować się po różnych jej stronach, przecinając ją nieskończoną ilość razy i przechodząc z jednej strony na drugą, jak np. w zad. 386 (3).

Przy wyznaczaniu asymptot korzysta się z następujących twierdzeń: a) jeżeli krzywa y === f(x) ma nieciągłość nieskończoną w punkcie x — a, czyli gdy y -> ±°o dla x -» a—0 lub dla .v -► a+0, to prosta x = a jest asymptotą pionową tej krzywej;

b) asymptoty nie pionowe (ukośne lub poziome), jeśli istnieją, mają równania o postaci y — kx-\-b, przy czym parametry k i b są określone wzorami

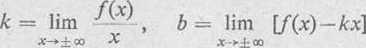
gdzie x w obu wzorach zachowuje się tak samo, tj. w obu wzorach x -> -f oo lub x -> —oo.

386. Wyznaczyć asymptoty krzywych :

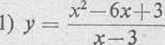
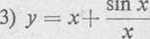
6)* y = Yx³—6x*

4) y = x arc ctg *    5) y = ln (4—x²)

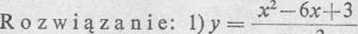
a)    Krzywa ma nieciągłość nieskończoną dla * = 3. Dlatego prosta x = 3 jest dla niej asymptotą pionową.

b)    Z kolei szukamy asymptot nie pionowych:

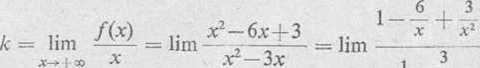
x

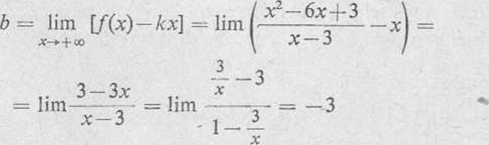
Podstawiając znalezione wartości k i b do równania y = kx+b otrzymamy równanie asymptoty ukośnej

Innych asymptot ukośnych krzyw^;a nie ma, ponieważ dla x -* — oo wartości k i b są takie same. Wykres krzywej przedstawiono na rys. 69.

2) y = xe^x

a)    Krzywa jest wszędzie ciągła, nie ma więc asymptot pionowych.

b)    Mamy

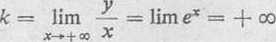
165