0018 2

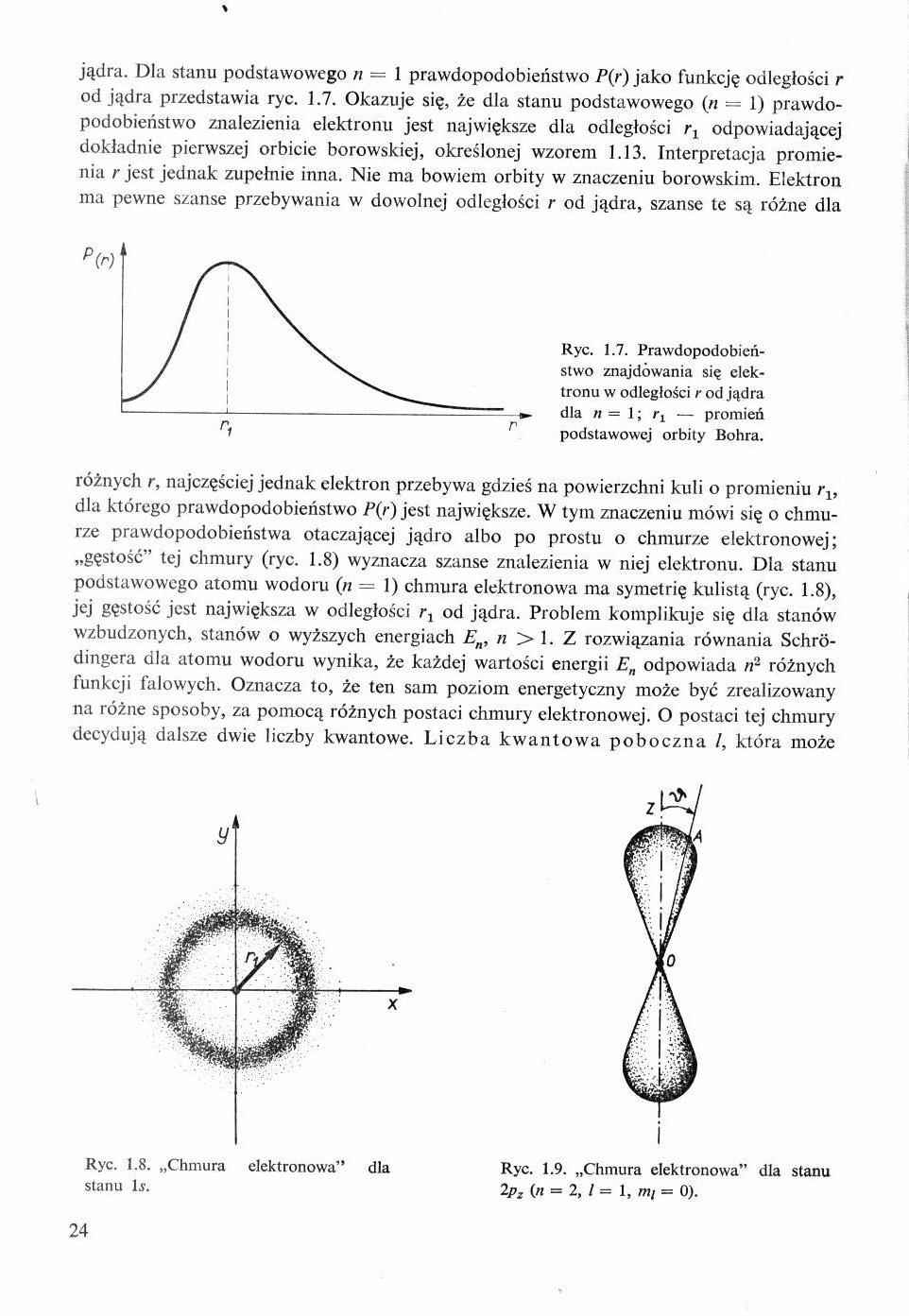
jądra. Dla stanu podstawowego n = 1 prawdopodobieństwo P(r) jako funkcję odległości r od jądra przedstawia ryc. 1.7. Okazuje się, że dla stanu podstawowego (n - - 1) prawdopodobieństwo znalezienia elektronu jest największe dla odległości r, odpowiadającej dokładnie pierwszej orbicie borowskiej, określonej wzorem 1.13. Interpretacja promienia r jest jednak zupełnie inna. Nie ma bowiem orbity w znaczeniu borowskim. Elektron ma pewne szanse przebywania w dowolnej odległości r od jądra, szanse te są różne dla

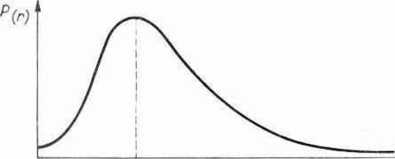
Ryc. 1.7. Prawdopodobieństwo znajdowania się elektronu w odległości r od jądra dla n = 1; z^-! — promień podstawowej orbity Bohra.

różnych r, najczęściej jednak elektron przebywa gdzieś na powierzchni kuli o promieniu r_lt dla którego prawdopodobieństwo P(r) jest największe. W tym znaczeniu mówi się o chmurze prawdopodobieństwa otaczającej jądro albo po prostu o chmurze elektronowej; „gęstość” tej chmury (ryc. 1.8) wyznacza szanse znalezienia w niej elektronu. Dla stanu podstawowego atomu wodom (n = 1) chmura elektronowa ma symetrię kulistą (ryc. 1.8), jej gęstość jest największa w odległości r, od jądra. Problem komplikuje się dla stanów wzbudzonych, stanów o wyższych energiach E_n, n >1. Z rozwiązania równania Sehró-dingera dla atomu wodoru wynika, że każdej wartości energii E_n odpowiada n² różnych funkcji falowych. Oznacza to, że ten sam poziom energetyczny może być zrealizowany na różne sposoby, za pomocą różnych postaci chmury elektronowej. O postaci tej chmury decydują dalsze dwie liczby kwantowe. Liczba kwantowa poboczna /, która może

y

X

Ryc. 1.8. „Chmura elektronowa” dla stanu 1a-.

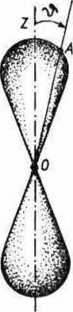
Ryc. 1.9. „Chmura elektronowa” dla stanu

2p_z (« = 2, / = 1, m, = 0).

24